Уравнение гармонического колебательного движения имеет вид 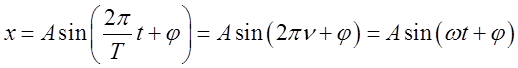 , где
, где ![]() - смещение точки от положения
равновесия, разное для разных моментов времени,
- смещение точки от положения
равновесия, разное для разных моментов времени, ![]() - амплитуда,
- амплитуда, ![]() - период,
- период, ![]() - начальная фаза,
- начальная фаза, ![]() - частота колебаний,
- частота колебаний, ![]() - круговая частота. Скорость и
ускорение точки, совершающей колебание, определяются соотношениями
- круговая частота. Скорость и
ускорение точки, совершающей колебание, определяются соотношениями 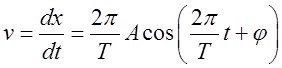 ,
, 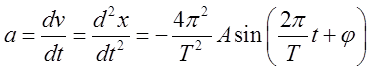 . Сила,
под действием которой точка массой
. Сила,
под действием которой точка массой ![]() совершает
гармоническое колебание,
совершает
гармоническое колебание, 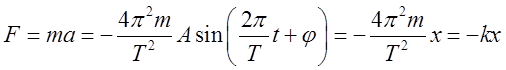 , где
, где
![]() , т.е.
, т.е. ![]() . Здесь
. Здесь ![]() - период колебаний точки,
совершающей колебания под действием силы
- период колебаний точки,
совершающей колебания под действием силы ![]() , где
, где ![]() - жесткость пружины, численно равная
силе, вызывающей смещение, равное единице. Кинетическая и потенциальная энергии
колеблющейся точки имеют вид
- жесткость пружины, численно равная
силе, вызывающей смещение, равное единице. Кинетическая и потенциальная энергии
колеблющейся точки имеют вид 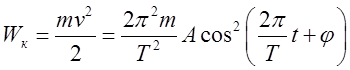 ,
, 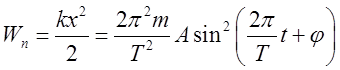 . Полная энергия
. Полная энергия 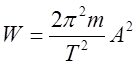 . Примером гармонических
колебательных движений могут служить малые колебания маятника. Период колебаний
математического маятника
. Примером гармонических
колебательных движений могут служить малые колебания маятника. Период колебаний
математического маятника ![]() . При
сложении двух одинаково направленных гармонических колебаний одинакового
периода получается гармоническое колебание того же периода с амплитудой
. При
сложении двух одинаково направленных гармонических колебаний одинакового
периода получается гармоническое колебание того же периода с амплитудой ![]() и с начальной фазой, определяемой
из уравнения
и с начальной фазой, определяемой
из уравнения 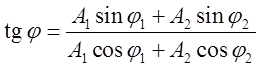 , где
, где ![]() и
и ![]() - амплитуды слагаемых колебаний,
- амплитуды слагаемых колебаний, ![]() и
и ![]() - их начальные фазы. При сложении
двух взаимно перпендикулярных колебаний одинакового периода уравнение
траектории результирующего движения имеет вид
- их начальные фазы. При сложении
двух взаимно перпендикулярных колебаний одинакового периода уравнение
траектории результирующего движения имеет вид 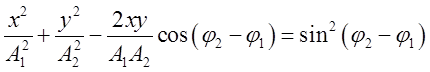 . Если на материальную точку массой
. Если на материальную точку массой ![]() , кроме упругой силы
, кроме упругой силы ![]() , действует еще мила трения
, действует еще мила трения ![]() , где
, где ![]() - коэффициент трения и
- коэффициент трения и ![]() - скорость колеблющейся точки, то
колебания точки будут затухающими. Уравнение затухающего колебательного
движения имеет вид
- скорость колеблющейся точки, то
колебания точки будут затухающими. Уравнение затухающего колебательного
движения имеет вид ![]() , где
, где ![]() - коэффициент затухания. При этом
- коэффициент затухания. При этом ![]() и
и ![]() , где
, где ![]() - круговая частота собственных
колебаний. Величина
- круговая частота собственных
колебаний. Величина ![]() называется
логарифмическим декрементом затухания. Если на материальную точку массой
называется
логарифмическим декрементом затухания. Если на материальную точку массой ![]() , уравнение колебаний которой дано в
виде
, уравнение колебаний которой дано в
виде ![]() , действует внешняя
периодическая сила
, действует внешняя
периодическая сила ![]() , то колебания
точки будут вынужденными и уравнение ее движения примет вид
, то колебания
точки будут вынужденными и уравнение ее движения примет вид ![]() , где
, где 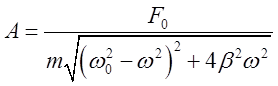 ,
, 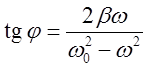 . Резонанс
наступает тогда, когда частота вынужденных колебаний
. Резонанс
наступает тогда, когда частота вынужденных колебаний ![]() связана с частотой собственных
колебаний
связана с частотой собственных
колебаний ![]() и с
коэффициентом затухания
и с
коэффициентом затухания ![]() соотношением
соотношением
![]() . При распространении
незатухающих колебаний со скоростью
. При распространении
незатухающих колебаний со скоростью ![]() вдоль
некоторого направления, называемого лучом, смещение любой точки, лежащей на
луче и отстоящей от источника колебаний на расстояние
вдоль
некоторого направления, называемого лучом, смещение любой точки, лежащей на
луче и отстоящей от источника колебаний на расстояние ![]() , дается уравнением
, дается уравнением 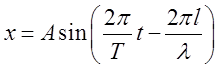 , где
, где ![]() - амплитуда колеблющихся точек,
- амплитуда колеблющихся точек, ![]() - длина волны. При этом
- длина волны. При этом ![]() . Две точки на луче на расстояниях
. Две точки на луче на расстояниях ![]() и
и ![]() от источника колебаний имеют
разность фаз
от источника колебаний имеют
разность фаз 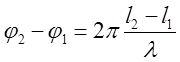 . При
интерференции волн максимум и минимум амплитуды получаются соответственно при
условиях
. При
интерференции волн максимум и минимум амплитуды получаются соответственно при
условиях 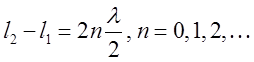 ,
, 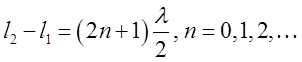 . Здесь
. Здесь ![]() - разность хода лучей.
- разность хода лучей.
Электромагнитные колебания и волны
Период ![]() электромагнитных
колебаний в контуре, состоящем из емкости
электромагнитных
колебаний в контуре, состоящем из емкости ![]() , индуктивности
, индуктивности ![]() и сопротивления
и сопротивления ![]() , определяется формулой
, определяется формулой 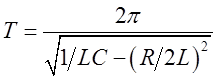 . Если сопротивление контура
настолько мало, что
. Если сопротивление контура
настолько мало, что ![]() , то период
колебаний
, то период
колебаний ![]() . Если
сопротивление контура
. Если
сопротивление контура ![]() не
равно нулю, то колебания будут затухающими. При этом разность потенциалов на
обкладках конденсатора меняется со временем по закону
не
равно нулю, то колебания будут затухающими. При этом разность потенциалов на
обкладках конденсатора меняется со временем по закону ![]() , если время отсчитывать от момента,
соответствующего наибольшей разности потенциалов на обкладках конденсатора.
Здесь
, если время отсчитывать от момента,
соответствующего наибольшей разности потенциалов на обкладках конденсатора.
Здесь ![]() - коэффициент
затухания. Величина
- коэффициент
затухания. Величина ![]() называется
логарифмическим декрементом затухания. Если
называется
логарифмическим декрементом затухания. Если ![]() , то колебания будут незатухающими,
и тогда можно записать
, то колебания будут незатухающими,
и тогда можно записать ![]() .
Если время отсчитывать от момента, когда разность потенциалов на обкладках
конденсатора равна нулю, то будет справедливым соотношение
.
Если время отсчитывать от момента, когда разность потенциалов на обкладках
конденсатора равна нулю, то будет справедливым соотношение ![]() . Закон Ома для переменного тока
записывается в виде
. Закон Ома для переменного тока
записывается в виде 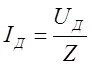 , где
, где ![]() и
и ![]() - действующие значения тока и
напряжения, связанные с их амплитудными значениями
- действующие значения тока и
напряжения, связанные с их амплитудными значениями ![]() и
и ![]() соотношениями
соотношениями ![]() ,
, ![]() ,
а
,
а ![]() - полное сопротивление
цепи. Если цепь содержит сопротивление
- полное сопротивление
цепи. Если цепь содержит сопротивление ![]() ,
емкость
,
емкость ![]() и индуктивность
и индуктивность ![]() , соединенные последовательно, то
, соединенные последовательно, то 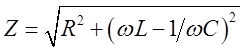 . При этом сдвиг фаз между
напряжением и током определяются формулой
. При этом сдвиг фаз между
напряжением и током определяются формулой 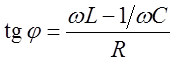 . Формулы для полного сопротивления
цепи
. Формулы для полного сопротивления
цепи ![]() и сдвига фаз
и сдвига фаз ![]() между напряжением и током при
различных способах включения сопротивления
между напряжением и током при
различных способах включения сопротивления ![]() , емкости
, емкости ![]() и индуктивности
и индуктивности ![]() : а)
: а) ![]() и
и ![]() включены последовательно:
включены последовательно: 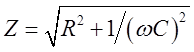 ,
, ![]() ; б)
; б)
![]() и
и ![]() включены параллельно:
включены параллельно: 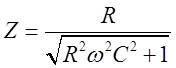 ,
, ![]() ; в)
; в)
![]() и
и ![]() включены последовательно:
включены последовательно: 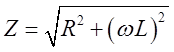 ,
, ![]() ; г)
; г)
![]() и
и ![]() включены параллельно:
включены параллельно: 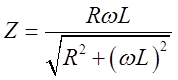 ,
, ![]() ; д)
; д)
![]() ,
, ![]() и
и
![]() включены последовательно:
включены последовательно:
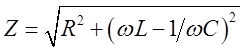 ,
, 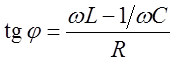 . Катушка,
обладающая сопротивлением
. Катушка,
обладающая сопротивлением ![]() и
индуктивностью
и
индуктивностью ![]() , в цепи
переменного тока соответствует последовательно включенным
, в цепи
переменного тока соответствует последовательно включенным ![]() и
и ![]() . Конденсатор с утечкой, т.е.
конденсатор, обладающий емкостью
. Конденсатор с утечкой, т.е.
конденсатор, обладающий емкостью ![]() и
сопротивлением
и
сопротивлением ![]() , соответствует
параллельно включенным
, соответствует
параллельно включенным ![]() и
и
![]() . Мощность переменного
тока
. Мощность переменного
тока ![]() .
.
По принципу Доплера частота ![]() света, воспринимаемая
регистрирующим прибором, связана с частотой
света, воспринимаемая
регистрирующим прибором, связана с частотой ![]() , посылаемой источником света,
соотношением
, посылаемой источником света,
соотношением 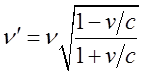 , где
, где ![]() - скорость регистрирующего прибора
относительно источника,
- скорость регистрирующего прибора
относительно источника, ![]() - скорость
распространения света. Положительное значение
- скорость
распространения света. Положительное значение ![]() соответствует удалению источника
света. При
соответствует удалению источника
света. При ![]() формулу
приближенно можно представить в виде
формулу
приближенно можно представить в виде  .
Расстояние между интерференционными полосами на экране расположенном
параллельно двум когерентным источникам света,
.
Расстояние между интерференционными полосами на экране расположенном
параллельно двум когерентным источникам света, 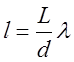 , где
, где ![]() - длина волны света,
- длина волны света, ![]() - расстояние от экрана до
источников света, отстоящего друг от друга на расстоянии
- расстояние от экрана до
источников света, отстоящего друг от друга на расстоянии ![]() (при этом
(при этом ![]() ). Результат интерференции света в
плоскопараллельных пластинках (в проходящем свете) определяется формулами:
усиление света
). Результат интерференции света в
плоскопараллельных пластинках (в проходящем свете) определяется формулами:
усиление света 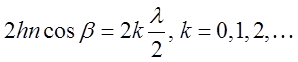 ; ослабление
света
; ослабление
света 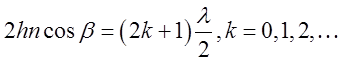 , где
, где ![]() - толщина пластинки,
- толщина пластинки, ![]() - показатель преломления,
- показатель преломления, ![]() - угол преломления,
- угол преломления, ![]() - длина волны света. В отраженном
свете условия усиления и ослабления света обратны условиям в проходящем свете.
Радиусы светлых колец Ньютона (в проходящем свете) определяются формулой
- длина волны света. В отраженном
свете условия усиления и ослабления света обратны условиям в проходящем свете.
Радиусы светлых колец Ньютона (в проходящем свете) определяются формулой ![]() ; радиусы темных колец
; радиусы темных колец 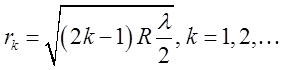 , где
, где ![]() - радиус кривизны линзы. В
отраженном свете расположение светлых и темных колец обратно их расположению в
проходящем свете. Положение минимумов освещенности при дифракции от щели, на
которую нормально падает пучок параллельных лучей определяется условием
- радиус кривизны линзы. В
отраженном свете расположение светлых и темных колец обратно их расположению в
проходящем свете. Положение минимумов освещенности при дифракции от щели, на
которую нормально падает пучок параллельных лучей определяется условием ![]() , где
, где ![]() - ширина щели,
- ширина щели, ![]() - угол дифракции,
- угол дифракции, ![]() - длина волны падающего света. В
дифракционной решетке максимумы света наблюдаются в направлениях, составляющих
с нормалью к решетке угол
- длина волны падающего света. В
дифракционной решетке максимумы света наблюдаются в направлениях, составляющих
с нормалью к решетке угол ![]() , удовлетворяющий
соотношению ( при условии, что свет падает на решетку нормально)
, удовлетворяющий
соотношению ( при условии, что свет падает на решетку нормально) ![]() , где
, где ![]() - постоянная решетки,
- постоянная решетки, ![]() - угол дифракции,
- угол дифракции, ![]() - длина волны падающего света и
- длина волны падающего света и ![]() - порядок спектра. Постоянная
решетки
- порядок спектра. Постоянная
решетки ![]() , где
, где ![]() - число щелей решетки, приходящееся
на единицу длины решетки. Разрешающая способность дифракционной решетки определяется
формулой
- число щелей решетки, приходящееся
на единицу длины решетки. Разрешающая способность дифракционной решетки определяется
формулой 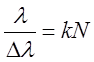 , где
, где ![]() - общее количество щелей решетки,
- общее количество щелей решетки, ![]() - порядок спектра,
- порядок спектра, ![]() и
и ![]() - длины волн двух близких
спектральных линий, еще разрешаемых решеткой. Угловой дисперсией дифракционной
решетки называется величина
- длины волн двух близких
спектральных линий, еще разрешаемых решеткой. Угловой дисперсией дифракционной
решетки называется величина ![]() .
Линейной дисперсией дифракционной решетки называется величина
.
Линейной дисперсией дифракционной решетки называется величина 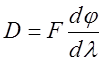 , где
, где ![]() - фокусное расстояние линзы,
проецирующей спектр на экран. При отражении естественного света от
диэлектрического зеркала имеют место формулы Френеля
- фокусное расстояние линзы,
проецирующей спектр на экран. При отражении естественного света от
диэлектрического зеркала имеют место формулы Френеля 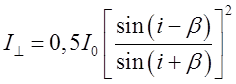 ,
, 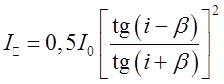 , где
, где
![]() - интенсивность световых колебаний
в отраженном луче, совершающихся в направлении, перпендикулярном к плоскости
падения света,
- интенсивность световых колебаний
в отраженном луче, совершающихся в направлении, перпендикулярном к плоскости
падения света, ![]() - интенсивность
световых колебаний в отраженном луче, совершающихся в направлении, параллельном
плоскости падения света,
- интенсивность
световых колебаний в отраженном луче, совершающихся в направлении, параллельном
плоскости падения света, ![]() - интенсивность
падающего естественного света,
- интенсивность
падающего естественного света, ![]() - угол
падения,
- угол
падения, ![]() - угол
преломления. Если
- угол
преломления. Если ![]() , то
, то ![]() . В этом случае угол падения
. В этом случае угол падения ![]() и показатель преломления
и показатель преломления ![]() диэлектрического зеркала связаны
соотношением
диэлектрического зеркала связаны
соотношением ![]() (закон
Брюстера). Интенсивность света, прошедшего через поляризатор и анализатор,
(закон
Брюстера). Интенсивность света, прошедшего через поляризатор и анализатор, ![]() (закон Малюса), где
(закон Малюса), где ![]() - угол между главными плоскостями
поляризатора и анализатора,
- угол между главными плоскостями
поляризатора и анализатора, ![]() - интенсивность
света, прошедшего через поляризатор.
- интенсивность
света, прошедшего через поляризатор.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.