Мы с Андреем не несем никакой ответственности за дальнейшее использование данных материалов. Все решения приводятся в символьном виде.
№1:
Условие: В идеальном колебательном контуре происходят собственные колебания тока согласно уравнению:
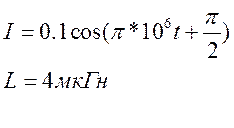
Найти зависимость от времени
энергии электрического поля в контуре (![]() ) - ?
) - ?
Решение:
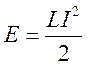
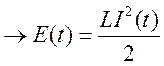
№2:
Условие: В упругой среде
распространяется плоская волна с амплитудой ![]() . Амплитуда
скорости частиц при этом
. Амплитуда
скорости частиц при этом ![]() . Найти
скорость волны, если …. (дальше условие неясно, но дано
. Найти
скорость волны, если …. (дальше условие неясно, но дано ![]() ).
).
Решение:
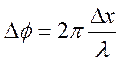 ;
; 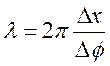 ;
; ![]() ;
; 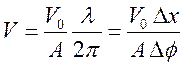
№3:
Условие: Материальная точка
совершает гармонические колебания с частотой ![]() . В
начальный момент времени она находится в положении равновесия и движется
равномерно со скоростью
. В
начальный момент времени она находится в положении равновесия и движется
равномерно со скоростью ![]() . Написать уравнение
колебаний.
. Написать уравнение
колебаний.
Решение:
![]() ;
; ![]() ;
; 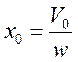 ;
; 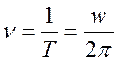 ;
;
![]() ;
;
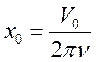 ;
; 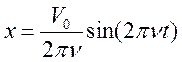
№4: Система совершает
затухающие колебания с частотой ![]() , логарифмический
декремент
, логарифмический
декремент ![]() . Найти промежуток времени, за который
энергия колебаний уменьшится в 10 раз.
. Найти промежуток времени, за который
энергия колебаний уменьшится в 10 раз.
Решение:
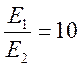 ;
; ![]()
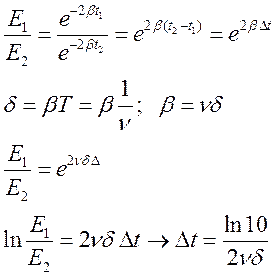
№5: Вдоль струны
распространяется поперечная гармоническая волна с частотой ![]() . Сила натяжения струны
. Сила натяжения струны ![]() . Определить линейную плотность струны, если разность
фаз колебаний равна
. Определить линейную плотность струны, если разность
фаз колебаний равна ![]() . При
этом дано
. При
этом дано
![]() .
.
Решение:
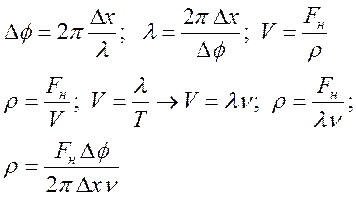 Здесь косяк с формулой скорости. Там вроде бы квадрат.
Здесь косяк с формулой скорости. Там вроде бы квадрат.
№6: Гиря массой ![]() подвешена на
пружине и совершает затухающие колебания. Определить период, если за время двух
колебаний амплитуда уменьшилась в 20 раз. Также дано:
подвешена на
пружине и совершает затухающие колебания. Определить период, если за время двух
колебаний амплитуда уменьшилась в 20 раз. Также дано: ![]()
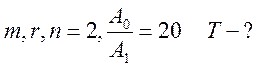
Решение:
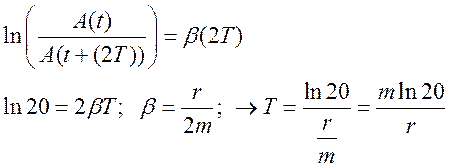
№7,8,9:
В колебательном контуре
действует ЭДС ![]() . Параметры
контура:
. Параметры
контура: ![]() .
. ![]() .
. ![]() .
.
7) Написать уравнение колебаний для напряжения на резисторе
8) Написать уравнение колебаний для напряжения на конденсаторе
9) Написать уравнение колебаний для заряда
Решение:
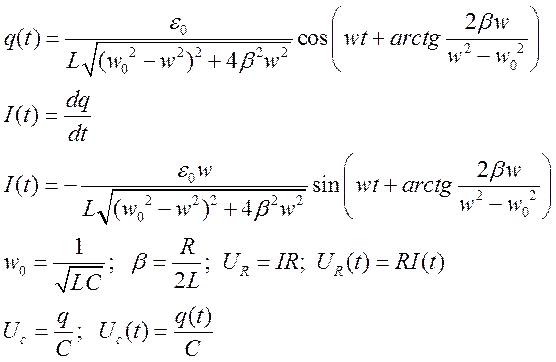
7) ![]()
8) ![]()
9) ![]()
№12:
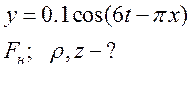
Требуется найти линейную плотность и импеданс.
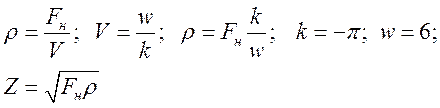 Здесь тоже какой-то косяк со скорость. Не понимаю.
Здесь тоже какой-то косяк со скорость. Не понимаю.
№13:
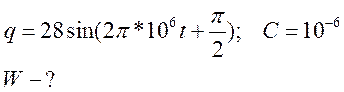
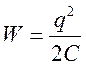
№14:
Дано: m, k, ![]() ,
, 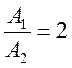 n - ?
n - ?
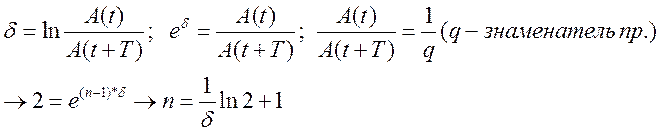
№15:
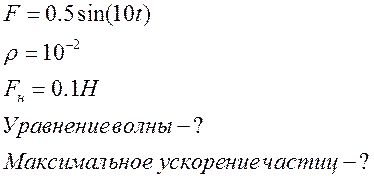
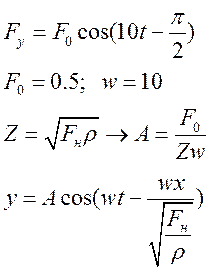
![]()
№16:
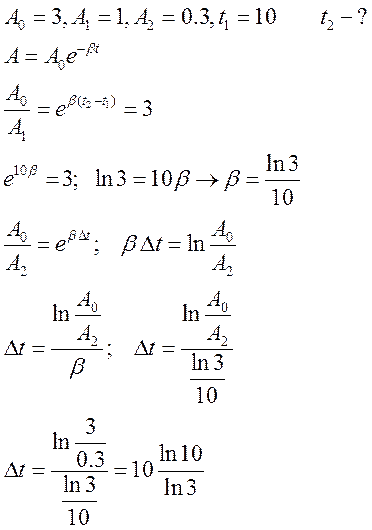
№17:
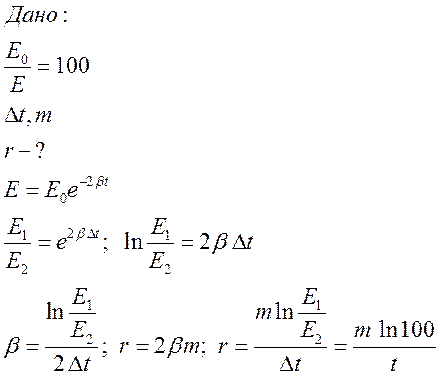
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.