Структурный анализ в решениях последовательных данных: Учебное пособие (Многовариантная алгоритмизация и применение сглаживающих фильтров. Теоретические основы структурного анализа), страница 9

На рисунке 1.4 изображена укрупненная схема типового блока фильтрации применительно к оцениванию возмущенного (в приращениях к опорному) движению ОУ по помехоискаженным сигналам измерительной информации x. За опорные сигналы x₀можно принимать математически определяемые программные траектории, задаваемые человеком-оператором уставки или результаты относительного сильного сглаживания предыстории движения ОУ, включая его входные, внутренние и выходные переменные. Измерительные сигналы в приращениях  характеризуют эти переменные в неполном числе и с помехами из-за не представительности точек замеров, различного рода наводок и т.п. В составе вектора (совокупности) измерений x могут быть и практически точные данные о действительных значениях регулирующих и некоторых возмущающих воздействиях ОУ, и тогда соответствующие компоненты вектора u_M приравниваются. Остальные же его компоненты формируются специальными корректирующими алгоритмами в функции от помехоискаженных отклонений между  и x.

Конкретизируем вариант постановки и решения задачи синтеза этих алгоритмов на основе математических схем оптимизации по критерию обобщенной работы.

В линейном приближении непрерывную модель возмущенного движения ЛА запишем в виде

                                  (1.17)

где a_M ,  b_M - векторы параметров (коэффициентов), t- непрерывное время, - вектор производных от фазовых координат  (разностные разновидности модели в дискретном времени представлены выражениями (1.13) - (1.15)).

Как уже отмечено, в составе вектора регулирующих сигналов могут быть хорошо контролируемые входные воздействия (в приращениях) самого ОУ. Их включение в модель делается известным путем и потому в дальнейшем условимся рассматривать только те компоненты u_M, которые надлежит формировать в зависимости от . Измеренные сигналы представим простой структурой

                                       (1.18)

в которой вектор  обозначает действительно фазовые координаты возмущенного (В) движения ОУ и соответствует искомым полезным сигналам, а вектор  - эквивалентным измерительным помехам. Они, в свою очередь, как уже отмечалось, отображаются смесью "обычных", статистически воспроизводимых случайных помех  и аномальных, грубых нестационарных помех. Последние подлежат особому учету и приводят к построению робастных (стабильных) фильтров, включающих своего рода автоматы ограничений.

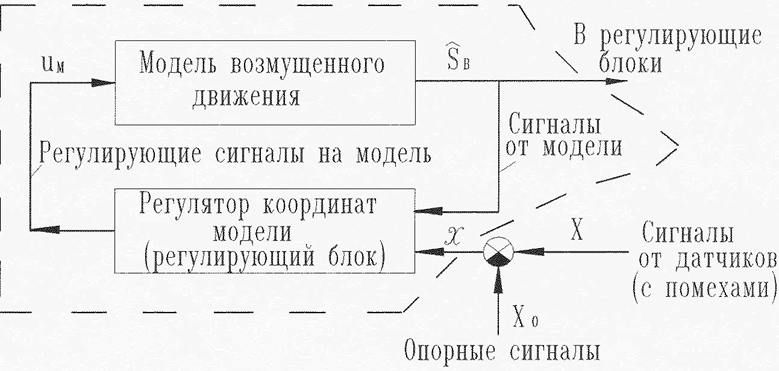
Рисунок 1.4 – Принципиальная схема фильтрации (координатного оценивания) сигналов возмущенного движения объекта управления (ОУ). Примечание: если помехи приложены к задающему входу системы управления (в том числе САР, САУ, АСУ), то используется упрощенная модель формирования самого задающего воздействия (в частности, по типу интегрального звена со входом u_м)

Критерий обобщенной работы для нетерминальной схемы зададим по аналогии с [10] интегральным квадратичным выражением

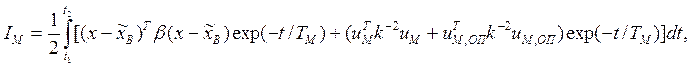                                                                                                            (1.19)

где x- входной сигнал в функции текущего времени t,  - оценка действительных значений фазовых координат возмущенного движения ОУ; u_M- координатное регулирующее воздействие на модель формирования полезного сигнала (см. рисунок 1.4); u_M,ОП- оптимальное регулирующее воздействие на входе исполнительного органа (блока), выходом которого является u_M;b, k^-2- диагональные матрицы коэффициентов, выбираемых сообразно, например, максимальным ошибкам датчиков и максимальным скоростям изменения действительных фазовых координат ОУ. Начало t₁ и конец t₂ скользящего интервала интегрирования и коэффициент T_M экспоненциальной весовой функции зависят от момента оценивания полезных сигналов, частотных свойств их и обычных, статистически воспроизводимых помех.

Приближенные значения этих настроек, как и других коэффициентов критерия типа (1.19), определяются по методикам [10], а затем подлежат уточнению в ходе функционирования системы.