![]() (3.2)
(3.2)
где m – интервал скольжения (сглаживания) – настроечный параметр.
2. Взвешенное скользящее среднее. При таком усреднении каждое значение рассматриваемой величины суммируется с весом, который увеличивается ближе к текущему моменту l.
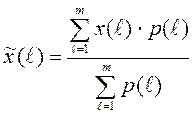 ,
(3.3) где p(l) – вес l-го усредняемого значения х(l), который равен l, т.е. при суммировании значений х(l), где l изменяется от 1 до m, веса также изменяются от 1 до m.
,
(3.3) где p(l) – вес l-го усредняемого значения х(l), который равен l, т.е. при суммировании значений х(l), где l изменяется от 1 до m, веса также изменяются от 1 до m.
3. Экспоненциальное скользящее среднее. Этот вид скользящего среднего в техническом анализе называется "экспоненциально приглаженным" [47]; как и в предыдущем случае, суммируемые данные взвешиваются, только веса здесь убывают по экспоненте, значения которой убывают по мере удаления от текущего момента усреднения:
![]() (3.4)
(3.4)
где ![]() -
скользящие экспоненциальные средние, полученные для l-го и (l - 1)-го отсчетов; α – коэффициент сглаживания
– настроечный параметр (он заключен в интервале то 0 до 1), который можно
оценить по соотношению [55]: α = 2 / (m+1).
-
скользящие экспоненциальные средние, полученные для l-го и (l - 1)-го отсчетов; α – коэффициент сглаживания
– настроечный параметр (он заключен в интервале то 0 до 1), который можно
оценить по соотношению [55]: α = 2 / (m+1).
В структурном анализе временных последовательностей технологических переменных (в технических системах) для текущего сглаживания используются операторы робастного сглаживания, которые "защищены" от аномальных погрешностей, имеющих место в данных анализируемого ряда. Данные, содержащие аномальные погрешности, легко распознать визуальным анализом, так как они резко отличаются от большинства значений на анализируемой реализации.
Одним из наиболее распространенных робастных сглаживателей является релейно-экспоненциальный первого порядка (РЭСI):
![]() (3.5)
(3.5)
![]() (3.6)
(3.6)
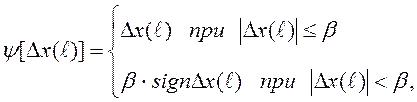 (3.7)
(3.7)
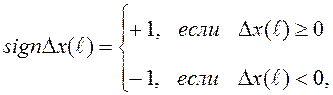 (3.8)
(3.8)
настроечный параметр α определяется, как и в экспоненциальном среднем: α =2 / (m+1), β ≈ │Δх*│+ 2σ, где Δх* – максимальное приращение полезного сигнала; σ - средне-квадратическое отклонение флуктуационной помехи.
Скользящие средние относятся к категории аналитических инструментов технического анализа, которые следуют за тенденцией. Цель их использования состоит в том, чтобы определить момент начала возникновения новой тенденции, а также сигнализировать о завершении тренда и его повороте. Скользящие средние предназначены для отслеживания тенденций в процессе их развития, но они не предназначены для прогнозирования движений на рынке в том смысле, в котором это делает графический анализ, поскольку всегда следуют за движением цен на рынке и сигнализируют о начале новой тенденции, но только после того, как она появилась [47]. По своей природе скользящие средние как бы отстают от динамики рынка. Причем, чем больше шаг скольжения, тем больше отставание. Так краткосрочное скользящее среднее (короткое) позволяет сократить отставание по времени по сравнению со средне- и долгосрочным скользящим средним (длинным), однако полностью его устранить невозможно. Короткие скользящие средние более чувствительны к динамике цен, чем длинные. На одних рынках целесообразнее использовать короткие скользящие средние, на других же длинные, как менее чувствительные.
На фьючерсных рынках часто используется простое скользящее среднее, которое строят на столбиковом графике, откладывая его значения по вертикали, что и цены соответствующего дня. Когда цена закрытия оказывается выше кривой скользящего среднего, поступает сигнал к покупке. Сигнал к продаже подается, когда цены опускаются ниже кривой скользящего среднего. Для более надежного подтверждения сигнала некоторые аналитики предпочитают подождать, пока кривая скользящего среднего после пересечения исходной реализации сама повернет в соответствующем направлении.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.