Структурный анализ в решениях последовательных данных: Учебное пособие (Многовариантная алгоритмизация и применение сглаживающих фильтров. Теоретические основы структурного анализа), страница 11

      (1.29)

Взяв производную от (1.29) по , имеем

откуда, произведя алгебраические преобразования, получаем искомый алгоритм

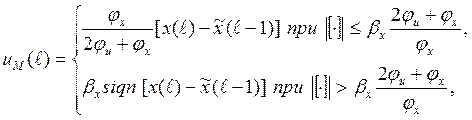                   (1.30)

который совместно с разностным уравнением (1.13) полностью характеризует фильтр как замкнутую САР (релейная часть есть вариант автомата ограничений). Отличие (1.30) от (1.21) в том, что (1.24) верно для дискретного времени и поэтому соответствующим образом производится выбор коэффициентов. Надлежащим выбором весовых коэффициентов j_x, j_u в исходном критерии по рекомендациям [20], с их дополнительной корректировкой в ходе моделирования и, главное, текущей адаптации фильтра обеспечиваются требуемые устойчивость и качество полученной системы.

Такого рода методические разработки имеют сходство с широко применяемыми в системах автоматического управления и автоматизированных системах управления технологическими процессами (АСУ ТП) так называемыми релейно-экспоненциальными фильтрами различных порядков [38], а также с  простыми нелинейными фильтрами Калмана [15]. Более понятными для приложений, по нашему мнению, являются интерпретации разрабатываемых робастных фильтров в рамках релейно-экспоненциального, медианно-экспоненциального и т.п. сглаживания временных рядов помехозащищенных данных и поэтому в дальнейшем будем использовать последние термины.

1.4 Алгоритмы робастной фильтрации

1.4.1 Алгоритм оценивания медианы

Одноступенчатое (сразу по всем L данным) оценивание медианы может быть представлено в виде

                              (1.31)

где med – обозначает операции оценивания медианы [20], которое заключается в следующем:

1.  Производится упорядочение отсчетов  по возрастанию их значений, т.е. строится вариационный ряд.

2. При нечетном L выбирается центральное (срединное) значение из упорядоченной последовательности.

3. При четном L определяется как полусумма из двух соседних (срединных) членов вариационного ряда.

Один из работоспособных фильтров для определения оценок  при наличии обычных и грубых (аномальных, с неустойчивыми статистическими свойствами) помех соответствует робастному варианту многократного экспоненциального сглаживания. При оценивании параметров степенного полинома второго порядка он имеет вид

                   (1.32)

                           (1.33)

                                 (1.34)

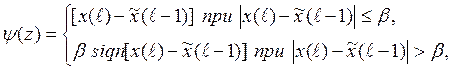                 (1.35)

или

    (1.36)

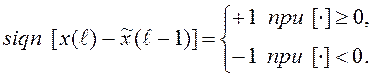                             (1.37)

где k={k₁, k₂, k₃,, b} -вектор настроечных коэффициентов (параметров);

m – интервал сглаживания.

Если y(z) рассчитывается по формуле (1.35), то получается релейно-экспоненциальный сглаживатель (РЭС), а если по формуле (1.36), то медианно-экспоненциальный сглаживатель (МЭС).

На рисунке 1.4 вектору u_M соответствуют компоненты u_M1=k₁y(z),   u_M2=k₂y(z), u_M3=k₃y(z).

Начальные значения настроечных коэффициентов робастного фильтра (1.32) - (1.37) можно находить по соотношениям

k₁=3a-3a²+a³,                                                  (1.38)

k₂=a²(2-a)                                                    (1.39)

k₃=a³,                                                         (1.40)

b=ôD_x÷+(2¸3)s_e ,                                              (1.41)

a=,                                                       (1.42)

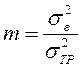,                                                       (1.43)

в которых - модуль вероятного приращения полезного сигнала на соседних отсчетах, s_ТР- требуемое среднеквадратичное отклонение расчетного подавления помехи. Формула (1.43) для определения числа осредняемых данных mсправедлива, если коэффициент автокорреляции обычной помехи e на соседних отсчетах меньше 0,3.

Уточнение настроечных коэффициентов (1.38) - (1.43) осуществляется с помощью, например, процедур симплексной поисковой оптимизации. Нестационарность коэффициентов полинома и помехи вызывает необходимость текущей адаптации настроечных параметров фильтров. В общем виде процедуру адаптации можно представить выражениями

                                            (1.44)