Структурный анализ в решениях последовательных данных: Учебное пособие (Многовариантная алгоритмизация и применение сглаживающих фильтров. Теоретические основы структурного анализа), страница 23

7. Моменты времени, когда происходит изменение тенденции реализации исследуемого ряда, можно определять путем сопоставления углов наклона кусочно-линейных аппроксимаций сигналана частично перекрывающихся участках. Выражения для соответствующей численной характеристики среднеквадратичной аппроксимации можно представить в виде

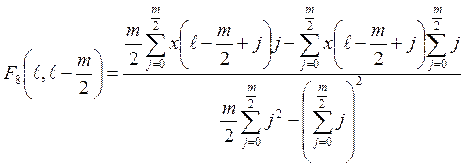              (2.37)

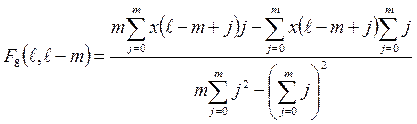                   (2.38)

8. Скачкообразные изменения в степени колебания исследуемой реализации переменной около тенденции хорошо выделяются с помощью выражения

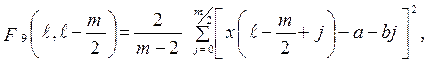                     (2.39)

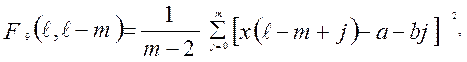                 (2.40)

представляющего собой оценку дисперсии сигнала относительно его линейной аппроксимации уравнением на интервалах в m и m/2 точек. Коэффициенты a и bопределяются методом наименьших квадратов [54].

9. В качестве показателя гладкости отрезков сигналов использованы аналоги характеристик, применяемых в теории сплайнов, например, вида

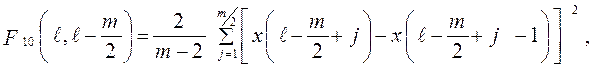        (2.41)

              (2.42)

при условии, что шаг дискретизации сигнала равен единице.

Предлагаемые методика и алгоритм оценивания структурных функций по типу многовариантного усреднения данных качественно полностью согласуются с прежними приемами структурного анализа рядов данных посредством сопоставления их количественных признаков на смежных не перекрывающихся участков данных одинаковой длины. Примеры использования функционалов отличия, рассчитанных на перекрывающихся отрезках, приведены в главе 4.

2.3 Выделение особых точек с помощью алгоритмов

                       адаптивного сжатия данных

При изучении нестационарных случайных сигналов важным является вопрос определения координат особых (поворотных) точек, после которых происходит существенная смена тенденции на реализациях переменных.

Описание текущего математического ожидания сигнала в интервалах времени между двумя соседними точками целесообразно производить на основе полиномиальных аппроксимаций. Фиксируя вид и степень полинома, можно получить сжатое описание динамики нестационарного случайного процесса путём запоминания координат особых точек. В отличие от способов, основанных на расчёте текущих статистических характеристик (спектральной плотности, автокорреляционной функции и др.) по данным одной реализации, предлагаемый метод описания нестационарных случайных сигналов оказывается более экономичным и несёт информацию о локальных изменениях динамики сигнала. Последнее даёт возможность восстановить исходную реализацию с заданной точностью.

Кроме того, знание координат особых точек позволяет перейти от описания динамики исходной реализации исследуемой переменной к описанию динамики особых точек, что в ряде случаев оказывается более простым делом. На этой основе возможно, в частности, изучение динамики фронтов нарастания и убывания сигнала и прогноз длительностей отдельных тенденций.

Удовлетворительные варианты описания нестационарных временных рядов можно получить на основе кусочно-линейной аппроксимации с адаптивной расстановкой узлов.

В задаче выделения особых (поворотных) точек много общего с задачей техники сжатия данных в современной телеметрии, целью которой является формирование минимального количества величин, обеспечивающих представление, в общем случае, непрерывного поведения переменной с заданной точностью.

При разработке алгоритма определения координат особых точек за основу был взят экстраполяционный алгоритм адаптивного сжатия данных со стыкующимися отрезками. У этого алгоритма адаптивным параметром является интервал аппроксимации при форсированном виде аппроксимирующего полинома. В общем случае использовался степенной полином первого порядка. Характерной чертой алгоритмов с адаптацией по интервалу аппроксимации является определение координат особых точек в реальном масштабе времени.

Блок-схема алгоритма выделения особых точек представлена на рисунке 2.14. Для начала его работы необходимо иметь три сглаженных значения реализации контролируемой переменной, что обеспечивается работой блоков 3 и 4.