Структурный анализ в решениях последовательных данных: Учебное пособие (Многовариантная алгоритмизация и применение сглаживающих фильтров. Теоретические основы структурного анализа), страница 12

                 (1.45)

в которых  - опорное значение настроечного параметра, равное, в частности, его начальной оценке по формулам (1.38) - (1.43), b_k, b_d- настроечные коэффициенты блока адаптации.

Конкретизируем выражения (1.32) - (1.43) для наиболее часто встречающихся на практике случаев.

1.4.2 Релейно-экспоненциальное сглаживание

первого порядка (РЭС I)

В случае использования модели сигнала первого порядка (1.13) и соответствующей конкретизации формул (1.32) - (1.37) в предположении , получаем типовую структуру РЭСI.

                                                                 (1.46)

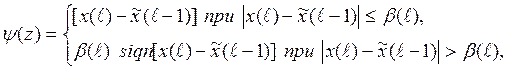            (1.47)

Оценка начального значения  может определяться медианным (по правилу скользящей выборочной медианы) осреднением предыдущих m данных по алгоритму (1.31). Настроечный параметр  (параметр сглаживания) является постоянной величиной и находится из условия (1.42), а  определяет свойства защищенности фильтра от влияния грубых помех, является постоянной величиной и находится из (1.41).

Для адаптивного РЭСI (АРЭСI) настроечные параметры  и  являются переменными и находятся по соотношениям

                                          (1.48)

                                          (1.49)

                    (1.50)

в которых настроечные параметры можно принимать

a*=,b^*=½D_x ½+(2¸3)s_N,                                    (1.51)

b_a=b_b=(2¸4),b_d=(0,2¸0,4).                                       (1.52)

Эти формулы получены из следующих соображений. Если остатки содержат в себе медленноменяющуюся составляющую, то сигнум-функция от них будет иметь тенденцию к преобладанию "+1" или наоборот "-1". По сглаженным значениям  сигнум-функции оперативно корректируются коэффициенты aи b. При наличии медленноменяющейся составляющей aи b увеличиваются, что увеличивает быстродействие фильтра и способствует уменьшению медленноменяющейся составляющей остатков. Величина коэффициента a^* рассчитывается по (1.51); коэффициента b^*  - исходя из правила «трех сигма»; причем s_N есть среднеквадратическое отклонение обычной помехи, а  - номинальное приращение полезного сигнала на смежных отсчетах; коэффициента b_a - из того, чтобы при b_d =(0,2 ¸ 0,4) величина a была меньше единицы, но больше нуля.

Целесообразно также адаптировать настроечные параметры  и  по скорости изменения оценки полезного сигнала. По аналогии с (1.50) такого рода показатель можно записать

                  (1.53)

где b_ck =(0,2 ¸ 0,4).

Тогда выражения (1.48) и (1.49) принимают вид

                                   (1.54)

                                   (1.55)

В частном случае b_a=b_a,ck; b_b =b_b,ck .

По аналогии можно вводить показатель (1.53) для адаптации параметров других робастных фильтров.

1.4.3 Релейно-экспоненциальное сглаживание

второго порядка (РЭС II)

В случае использования модели сигнала второго порядка (1.14) и конкретизации формул (1.32) - (1.37) в предположении , получаем структуру РЭС II

                                (1.56)

                                       (1.57)

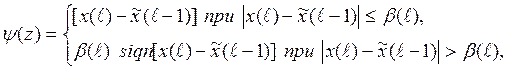            (1.58)

                             (1.59)

Оценка начального значения  может определяться по алгоритму (1.31), а оценка начального значения  по выражению

.               (1.60)

Настроечные параметры  и  для РЭС II являются постоянными, а для АРЭС II  адаптируются по алгоритмам (1.48) - (1.50).

1.4.4 Релейно-экспоненциальное сглаживание

третьего порядка (РЭС III)

Выражения алгоритмов РЭС III представлены зависимостями (1.32) - (1.35), а настроечных параметров - (1.38) - (1.43). Оценка начальных значений  и  вычисляется по формулам (1.31), (1.60), а оценка начального значения - по соотношению

                                                                                       (1.61)

Настроечные параметры  и  для РЭС II являются постоянными. Для адаптивного РЭС III настроечные параметры  и  вычисляются по формулам (1.48) - (1.50).

1.4.5 Медианно-экспоненциальное сглаживание

первого порядка (МЭС I)