Структурный анализ в решениях последовательных данных: Учебное пособие (Многовариантная алгоритмизация и применение сглаживающих фильтров. Теоретические основы структурного анализа), страница 5

Утверждение 1. Задача сглаживания одномерных динамических сигналов (рядов данных) x_j с оптимизацией учитывающих разброс остатков  и изменчивость оценок  квадратичных критериев

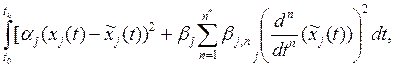                       (1.5)

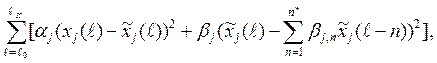                      (1.6)

при заданных значениях

           (1.7)

является эквивалентной по отношению к детерминированной линейной задаче следящего регулирования в рамках структурного представления, согласно которому корректирующие координатные управления  входят в, трактуемую как основное ограничение, управляемую модель формирования оценок

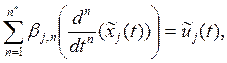                                        (1.8)

                                    (1.9)

и по этим выражениям замещают в критериях (1.5), (1.6) вторые их слагаемые.

Использованный в (1.5) обобщенный показатель изменчивости оценок  соответствует функционалу сложности непрерывных n^* раз дифференцируемых кривых - функций времени [14]. Из него, в частности, получаются составляющие критериев (1.1), (1.3), а именно – при n^*=1, b_j,1=1, имеем и при n^*=2, b_j,2=1, имеем . По аналогии с указанным источником этот функционал можно дополнить желаемой опорной траекторией  и распространить его на  многомерные  динамические сигналы. Дискретный вариант показателя изменчивости оценок в (1.6) содержит в себе слагаемые из (1.2), (1.4) и допускает еще более гибкие обобщения. Практическим подтверждением чему служат результаты построения многих сглаживающих фильтров.

Модель (1.8), (1.9) полностью вписывается в математические схемы объектов регулирования, детально рассмотренные в [18, 30, 31] применительно к детерминированной линейной задаче оптимального отслеживания заданного сигнала, которому здесь сопоставлен подлежащий сглаживанию сигнал x_j. Помехоискаженность[6] последнего учитывается путем занижения значений весового коэффициента a_j, относительно значений b_j сообразно предполагаемым и последовательно уточняемым дисперсиям помех и изменений полезной компоненты.

Утверждение 2. Многовариантные по преобразованиям (многоструктурные) сглаживающие фильтры, включая все формы, например, релейно-экспоненциального и медианно-экспоненциального сглаживания различных порядков[7], соответствуют по своему строению результатам локальной (усеченной) оптимизации в классе критериев общего вида [42]

                         (1.10)

с конечношаговой (на )экстраполяцией последовательности оценок  медленноменяющейся составляющей сглаживаемого ряда данных x(1), x(2),…,x(L) и соответствующей приближенной заменой (1.10) на выражение

            (1.11)

при известных значениях для  и  для  и при выбранном правиле экстраполяции  с подстановкой в (1.11).

В относительно простом случае локальной оптимизации по выражению 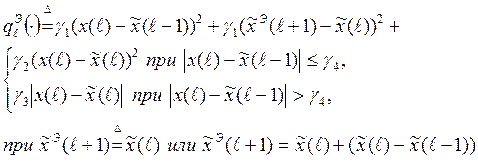(1.12)

с подстановкой в (1.12), последующим дифференцированием и приравниванием выражения производной нулю получаются решения типа релейно-экспоненциальных фильтров с настроечными параметрами g₁,…,g₄.

Подобным образом возможно обобщить и усовершенствовать многие другие разработки в связи с математико-техническим обеспечением автоматизированных систем. Разнообразные примеры этому содержатся в [33, 34]. В частности, разработанные управляемые фильтры включены во все процедуры проверки достоверности и предварительной обработки сигналов измерительной информации. При этом, как и в других специализированных схемах, приходится привлекать разнообразные вспомогательные операторы с наращиванием многовариантности систем.

Алгоритм предварительной обработки сигналов. Назначение алгоритма: опрос автоматических датчиков, первичная проверка достоверности поступивших данных, определение оценок сигнала и его производных, а также сопутствующих логических признаков по результатам перечисленных действий.

В изложении используются следующие термины.

Значение сигнала - величина сигнала прошедшего первичную проверку достоверности.

Таблица 1.1 – Некоторые алгоритмы сглаживания одномерного

дискретного сигнала