Структурный анализ в решениях последовательных данных: Учебное пособие (Многовариантная алгоритмизация и применение сглаживающих фильтров. Теоретические основы структурного анализа), страница 26

Приведем постановки названных выше задач.

2.5.1 Постановка задачи построения условно-образцовой

 кривой

       Дано:

1. Реализация временной последовательности значений анализируемой переменной х(l),  l = 1,2,…, L.

2. Метод построения тренда (условно-образцовой кривой), например, скользящее арифметическое среднее в виде

             ,                (2.48)

где – m настроечный параметр (величина отрезка скольжения). Причем рассчитанное на каждом шаге значение скользящего среднего ставится в центр отрезка шириной m.

3. Критерий К в виде двухкомпонентного показателя для настройки величины m, содержащий точностную и гладкостную составляющие в соответствии с (2.37) и (2.38), который берется в виде:

            ,                                    (2.49)

                                                (2.50)

где –  нормированные значения показателей гладкости и точности;   - весовые коэффициенты.   

4. Ограничения на интервал поиска величины m:  .

Требуется:

1. Найти оптимальный настроечный параметр m скользящего арифметического среднего, при котором двухкомпонентный критерий принимает максимальное значение.

2. Построить условно-образцовую кривую на исходной реализации переменной х(l) с использованием скользящего арифметического среднего с оптимальной настройкой m.

3. Изобразить условно-образцовую кривую в графической форме с указанием на ней особых точек.

Под условно-образцовой кривой понимается такая трендовая составляющая сигнала х(l), которая наилучшим образом удовлетворяет двухкомпонентному критерию.

Двухкомпонентный критерий, как было сказано ранее, содержит гладкостную  и точностную  составляющие, которые  равны:

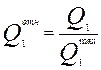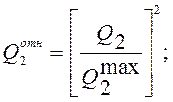;                                      (2.51)

где –  максимальные значения гладкостной и точностной составляющих.

В соответствии с (2.27) гладкостная составляющая  равна:

                                                     (2.52)

где -   сглаженные значения величины х, взятые в (l)- й момент отсчета и сдвинутые в прошлое на один и два шага по отношению к моменту (l).

Точностная составляющая критерия  в соответствии с (2.38) взята в виде среднемодульного значения:

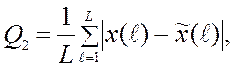                                                                         (2.53)

где – L число значений х в реализации, т.е. длина рассматриваемого ряда.

 оценивается как среднемодульное значение вторых разностей исходного ряда данных х(l), l = 1,2,…, L:

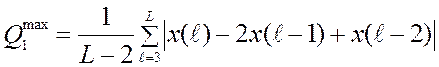           ;                           (2.54)

 оценивается как cреднемодульное отклонение значений исходного ряда данных х(l) от общего среднего , которое определяется как обычное среднее выборочное значение:

                                          .                                    (2.55)

2.5.2 Постановка задачи выбора оптимальных настроек

 методов структурного анализа рядов данных

     Дано:

1. Условно-образцовая кривая с выделенными на ней особыми точками.

2. Известные методы структурного (включая и методы технического) анализа.

3. Среднемодульный критерий в виде:

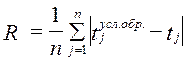                                                 ,                               (2.56)

где  - временная координата j-ой особой точки на условно-образцовой кривой; t_j – временная координата j-ой особой точки, найденной с помощью какого-либо метода структурного анализа; n - число особых точек, обнаруженных на условно-образцовой кривой.

4. Ограничения на интервал поиска оптимальных настроек:  

Требуется:

1.  Найти такие настроечные параметры методов структурного анализа, при которых R →  min.

2. Использовать методы структурного анализа с оптимальными настройками для выделения особых точек на реализациях данных, характеризующих работу технических и рыночных объектов.

Задача поиска оптимальных настроек решается методом перебора значений настроечных параметров в окрестности их начальных величин с учетом ограничений на область поиска. Начальные значения могут быть найдены либо эмпирически, либо взяты из монографий по техническому анализу, например, из [46].