Структурный анализ в решениях последовательных данных: Учебное пособие (Многовариантная алгоритмизация и применение сглаживающих фильтров. Теоретические основы структурного анализа), страница 10

В силу возможного появления аномальных помех предлагаем в дополнение к структурам (1.17) - (1.19) и аналогичным математическим схемам известных разработок [3, 20] явные ограничивающие условия, в частности, вида

½u_M(t)½£ A                                                (1.20)

с тем, чтобы обеспечить принадлежность свойств модельных оценок полезных сигналов физически реальным областям. Прикладное обоснование данного дополнения содержится в разделах, посвященных моделированию и полунатурным испытаниям робастных фильтров.

Сообразно типовой схеме риcунка 1.4, конкретизированной выражениями (1.17) - (1.20), задача синтеза корректирующего алгоритма заключается в установлении такой зависимости u_M(t) от  и x(t), которая минимизирует (min) критерий обобщенной работы при соблюдении  введенных ограничений. Наиболее практичным является алгоритм, оптимальный в строго локальном смысле [20]. На основе известного решения такого рода задачи [20] и при дополнительном учете (1.20) получаем

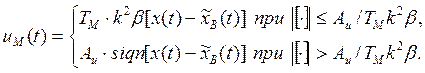                       (1.21)

В адаптивном варианте обобщенный коэффициент k_об=T_Mk²b поднастраивается на основе оперативного совместного анализа остатков  и скоростей . Пример раздельного анализа последних с целью уточнения ковариационной матрицы ошибок оценивания рассмотрен в [20], но для улучшения результатов, особенно в присутствии аномальных помех, это обоснованнее делать совместно с анализом остатков. Для такого рода поднастройки в развитие математической схемы из [20] используется алгоритм параметрической адаптации

                                    (1.22)

                          (1.23)

                      (1.24)

где вспомогательные коэффициенты  выбираются с учетом общих положений [20] и по результатам моделирования и полунатурных испытаний.

В выражении (1.22) составляющая (1.23) соответствует известной структуре из [20]. Составляющая же (1.24) получена из условия изменчивости остатков с приближением их свойств к "белой" последовательности, для которой показатель (1.24) близок к нулю.

В ориентации на широкое применение цифровой техники в исследовательских и непосредственно рабочих целях приведем детальные результаты для  фильтров, записанных на  языке разностных уравнений. Они получены в соответствии с дискретными аналогами структур типа (1.21) - (1.24) и некоторых дополнительных структур, в том числе частного вида для систем невысокого порядка. Поясним это на примере частичного синтеза регулирующего блока в составе робастного фильтра типа релейно-экспоненциального сглаживания первого порядка.

Для случая дискретного времени, и простейшей скалярной структуры (1.13) квадратичный вариант критерия обобщенной работы принимает вид

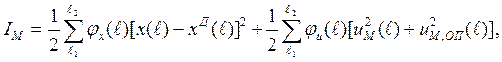                (1.25)

где весовые коэффициенты j_x, j_u соответствуют сомножителям  и  выражения (1.19) с учетом шага квантования t. Полагая оптимальным регулирующий блок фильтра, имеем u_M=u_{M, ОП}, и в ориентации на одношаговую локальную оптимизацию в сочетании с автоматами ограничений получаем следующую задачу синтеза алгоритма регулирования для схемы рисунка 1.4.

Дано: 1. Схема фильтра как следящей системы автоматического регулирования. 2. Модель формирования оценок полезного сигнала (1.13). 3. Входной сигнал (1.16). 4. Ограничения на сложность алгоритма искомого регулирующего блока (в классе операторов минимальной "памяти", которые обусловлены, собственно, ориентацией на одношаговую оптимизацию). 5.Одношаговый критерий для каждого дискретного - го отсчета

                                     (1.26)

при ограничениях на изменения выдаваемых оценок, к примеру, типа

                                      (1.27)

сообразно диапазону значений первого приращения самого полезного сигнала.

Требуется: построить алгоритм А выработки модельных регулирующих воздействий

                                         (1.28)

минимизирующий (min) критерий (1.26) при условии (1.27).

Решение такой задачи состоит в раскрытии структуры (1.28), исходя из выражений