Структурный анализ в решениях последовательных данных: Учебное пособие (Многовариантная алгоритмизация и применение сглаживающих фильтров. Теоретические основы структурного анализа), страница 21

4)  определение локальных экстремумов на реализациях функционала отличия;

5)  сравнение ординат локальных экстремумов с зоной нечувствительности;

6)  запоминание координат особых точек.

При определении координат особых точек с помощью функционалов отличия важно правильно выбрать длину скользящего “окошка” m охватывающего два смежных интервала длительностью в m/2 точек, для которых рассчитываются численные характеристики F. Одним из приемлемых способов решения этого вопроса является обучение с учителем, когда величина m, а также пороговые значения функционалов отличия определяются на основе минимизации ошибок выделения особых точек, указанных учителем.

В общем случае выделение моментов совместного изменения определённых свойств набора случайных величин возможно на основе анализа реализаций скалярного функционала отличия, представляющего собой сумму взвешенных разностей конкретных численных характеристик на соседних интервалах времени, определённых для каждой случайной величины.

Рассмотрим некоторые функционалы отличия, применявшиеся в работе для описания структуры реализаций контролируемых переменных.

1.  Выделение момента ступенчатого изменения уровня сигнала x(l) возможно на основе сравнения средних значений двух соседних участков x(l), характеризуемых значениями признака F₁,

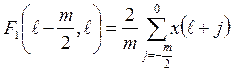                             .                                    (2.26)

Аналогично рассчитывается величина F₁(l ,l+ m/2), необходимая для определения функционала по формуле (2.25).

Разность средних уровней на соседних участках имеет более плавный характер реализаций по сравнению с графиком исследуемых данных x(l). По виду графиков функционала Ф(l) легче судить о происходящих изменениях в тенденции процесса. Интегральный характер преобразования позволяет частично отфильтровывать сильные колебания регистрируемых данных около тенденции. На рисунке 2.4 приведён пример реализации приведённого возмущения по содержанию кремния в чугуне на выпусках из доменной печи и функционала Ф₁(l).

Из рисунка видно, что локальные экстремумы на графике Ф₁(l) приходятся на моменты ступенчатого изменения тенденции приведённого возмущения. Задаваясь величиной зоны нечувствительности, можно выделять только скачки с определённой разностью уровней.

2.  Моменты времени, когда происходит изменение тенденции реализации исследуемой переменной, можно определять путём сопоставления углов наклона кусочно-линейных аппроксимаций сигнала x(l) на соседних участках.

Рисунок 2.4 – Выделение особых точек с помощью функционала Ф₁

Выражения для соответствующей численной характеристики F₂ среднеквадратичной аппроксимации можно представить в виде

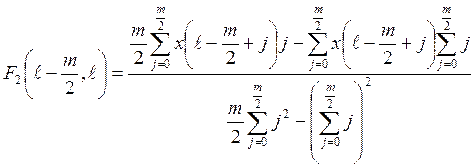,               (2.27)

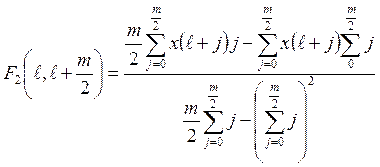.                       (2.28)

График функционала Ф₂(l) для приведённого возмущения по содержанию кремния в чугуне на выпусках из доменной печи приведён на рисунке 2.5.

Варьированием зоны нечувствительности для функционала можно добиться выделения только существенных изменений тенденции сигнала.

Рисунок 2.5 – Выделение особых точек с помощью функционала Ф₂

3.  Скачкообразные изменения степени колебания исследуемой реализации переменной около тенденции хорошо выделяются с помощью выражения

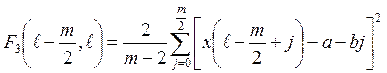,                   (2.29)

представляющего собой оценку дисперсии сигнала х относительно его линейной аппроксимации уравнением  на интервале в m/2 точек. Коэффициенты а и b определяются методом наименьших квадратов. Значение F₃(l,l+m /2) вычисляется по формуле, аналогичной (2.29). Пример выделения моментов изменения степени колебания функционалом Ф₃(l) показан на рисунке 2.6.

Рисунок 2.6 – Выделение особых точек c помощью функционала Ф₃

4.  Выделение моментов времени изменения статистических свойств динамического сигнала возможно на основе статистик, рассматриваемых в [45]. Для дискретного сигнала их можно записать в виде

                                    ,                                      (2.30)