Структурный анализ в решениях последовательных данных: Учебное пособие (Многовариантная алгоритмизация и применение сглаживающих фильтров. Теоретические основы структурного анализа), страница 7

1.2 Исходные положения по фильтрации

Важными элементами САР, САУ, АСУ, АОС, АСНИ являются сглаживающие фильтры. Такие фильтры используются в основном контуре, блоке предварительной обработки задающего сигнала, а также в различного рода контурах адаптации. Реальные условия их работы являются чаще всего нестабильными в смысле статистических свойств помех и самих полезных сигналов. Поэтому традиционные схемы фильтрации, предполагающие хорошую предсказуемость таких свойств, оказываются недостаточно работоспособными (в частности, весьма чувствительными к вариациям вида распределения и аномальным данным). В последнее время возрастающее внимание уделяется так называемым робастным (стабильным, грубым) статистическим процедурам, которые обладают устойчивостью по отношению к вариациям исходных предпосылок по свойствам полезных сигналов и помех.

Состояние дел в указанной области таково, что требуются разнообразные теоретические и практические разработки применительно к конкретным модельным и реальным ситуациям. В настоящем разделе рассмотрены некоторые из конкретных разработок.

Для конкретности рассмотрим постановку и решение задачи частичного синтеза[9] и сравнительного анализа тех вариантов робастных фильтров, прототипом которых являются схемы фильтров Винеpа, Заде-Pагоццини, Кальмана-Бьюси и Луенбеpгеpа, в простых случаях типа инерционных и форсирующих звеньев. Такие фильтры входят в состав тех САР, АСУ, АОС, АСНИ, которые выбраны как базовые системы-прототипы в настоящей работе.

Постановка задачи

Дано:

1. Общая структура фильтров как замкнутых САР по типу схем, описанных в трудах [10, 12], где условным объектом регулирования является модель формирования полезного сигнала, входным воздействием - поступающий от датчика помехоискаженный полезный сигнал, выходным воздействием - оценка полезного сигнала на выходе координатно регулируемой модели, а регулятором (управляющим устройством) - искомый блок.

2. Конкретные модели формирования оценок полезного сигнала, например, в виде рекуррентно-разностных уравнений

- первого порядка

                                          (1.13)

- второго порядка

                                         (1.14)

- третьего порядка

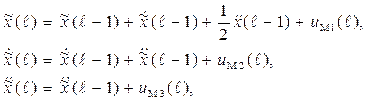                          (1.15)

где  - сглаженные значения результата измерения как оценки скалярного полезного сигнала (в случае векторного полезного сигнала аналогичные выражения записываются для всех его компонентов); -дискретное время, - координатное регулирующее воздействие на модель формирования полезного сигнала (, как и другие ,  компоненты регулирующего воздействия, для моделей каждого порядка вырабатываются соответствующим образом);  - дискретные оценки первой производной (скорости) изменения полезного сигнала  - дискретные оценки второй производной (ускорения) изменения полезного сигнала . Уравнения (1.13) - (1.15) положены в основу построения описываемых далее фильтров.

3. Схема представления помехоискаженного сигнала датчика (входного сигнала фильтра)

                                       (1.16)

в которой - действительный полезный сигнал, - обычная, статистически воспроизводимая помеха, в частности, типа белого шума с нормальным распределением, - эпизодически действующая помеха с плохо предсказуемыми статистическими свойствами, в частности, типа аномальных (грубых) выбросов. Последние могут характеризоваться интервально заданной вероятностью появления значений, существенно превышающих среднеквадратическое отклонение  обычной помехи. По результатам обобщения [15] указанная вероятность находится в пределах 0,05¸0,20 и является нестабильной. Типичная особенность реальных полезных сигналов заключается в том, что они ограничены по уровню, скоростям изменения и ускорениям и использование этой информации в составе фильтров обеспечивает повышение надежности и точности их работы.

4. Ограничения на сложность фильтров по техническим условиям их программной и аппаратурной реализации. В настоящей работе рассматривается класс фильтров со сложностью, близкой к хорошо зарекомендовавшим себя фильтрам в реальных САР, САУ, АСУ, АОС, АСНИ.