Структурный анализ в решениях последовательных данных: Учебное пособие (Многовариантная алгоритмизация и применение сглаживающих фильтров. Теоретические основы структурного анализа), страница 20

Метод компонентной фильтрации предполагает, что исследуемый случайный процесс относится к классу нестационарных случайных процессов с обобщёнными стационарными приращениями. Предполагается, что реализация нестационарного случайного процесса задана на интервале времени (0÷Т) и допускает разложение на два вида компонент: первый из них является стационарным случайным процессом типа белого шума, второй – нестационарным изменением текущего математического ожидания, допускающим разложение по некоторой системе базисных функций.

Способ компонентной фильтрации основан на разложении случайного процесса посредством последовательного многократного применения оператора текущего усреднения на слабо коррелированные составляющие.

Алгоритм компонентного разложения имеет следующий вид.

1.  Исходный случайный процесс подвергается обработке линейным оператором текущего усреднения. Число усредняемых данных m подбирают таким образом, чтобы обеспечить минимальную корреляцию между сглаженной реализацией  и высокочастотной компонентой Δ₁х(), определяемой из выражения

,                                      (2.20)

где 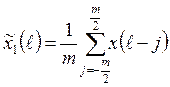                                    .                                        (2.21)

2.  Дальнейшей обработке подвергается относительно низкочастотная составляющая . На этом этапе параметры оператора текущего усреднения подбираются так, чтобы минимизировать корреляцию между компонентами Δ₁х(l) и Δ₂х(l), где

.                                    (2.22)

Величина  определяется аналогично . Затем информация извлекается из  и т.д.

3.  В результате разложения образуется последовательность центрированных компонент в виде

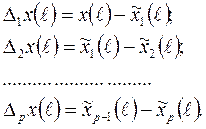                                     (2.23)

Окончательное выражение для компонентного разложения принимает вид

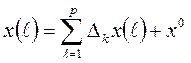,                                      (2.24)

где x⁰ – постоянный уровень процесса х(l).

Недостатком этого метода является разложение в общем случае по коррелированным компонентам. Однако он привлекает к себе внимание простотой анализа и физической наглядностью. За счёт операций многократного сглаживания увеличивается точность сглаживания. Метод прост в реализации на ЭВМ, хотя и имеет значительный объём вычислений.

2.2.3 Выделение особых точек с помощью функционалов отличия

Описание однородности структуры случайных сигналов во времени осуществляется путём фиксирования особых точек, которые соотносятся с моментами наиболее значительного изменения конкретных свойств случайного сигнала.

Для определения координат особых точек целесообразно применять методы локального анализа изображений. Моменты изменения определённых свойств сигнала находятся на основе анализа реализаций соответствующих функционалов отличия

                   ,                              (2.25)

представляющих собой разность численных значений некоторых характеристик F(l) двух соседних скользящих участков длительностью в m/2 точек случайного процесса. Введение этих функционалов позволяет получить реализации информативных признаков в том смысле, что локальные экстремумы на графиках Ф(l), превышающие по своему значению зоны нечувствительности, позволяют определить местоположение и вид особых точек на реализациях первичных данных.

При формировании функционалов отличия полезно ориентироваться на идеи теории структурных связей с явным временем, когда структурные связи подбираются из условия инвариантности относительно неинформативных, с точки зрения поставленной задачи исследования, параметров сигнала. При обработке сильно зашумлённой информации предпочтение следует отдавать интегральным преобразованиям исходных данных.

Алгоритм определения моментов изменения свойств реализаций контролируемых данных на основе методов локального анализа временных рядов можно представить в виде следующей последовательности действий:

1)  постановка задачи исследования;

2)  выбор функционала отличия;

3)  расчёт реализации функционала;