Структурный анализ в решениях последовательных данных: Учебное пособие (Многовариантная алгоритмизация и применение сглаживающих фильтров. Теоретические основы структурного анализа), страница 3

Начнем с задач и результатов синтеза типовых фильтров, используемых во всех наших разработках. Главное внимание уделим стабильному (робастному) многовариантному сглаживанию одномерных (скалярных) и многомерных (векторных) первичных и расчетных динамических сигналов (рядов данных) в непрерывной и дискретной формах[2]. В качестве общетеоретической основы приняты известные труды [1, 9 - 14]. Прикладные работы по стабильному (в сущности, нелинейному) сглаживанию сигналов все еще сдерживаются фактически и освещаются весьма мало (по сравнению с областью линейных фильтров) в доступных зарубежных и отечественных публикациях [15].

Полагаем принципиально важным тезис [16] о необходимости постановок и решений задач синтеза сглаживающих фильтров, опираясь на согласованное с конкретными условиями критериально-ограничительное описание подлежащих выделению медленноменяющихся составляющих (полезных сигналов, трендов) и подлежащих отделению быстроменяющихся составляющих (помеховых сигналов, шумов) исходных динамических сигналов. Другими словами, суть соответствующих исследований в том, чтобы с помощью критериев и ограничений адекватно формализовать желаемые свойства реализаций оценок  и остатков , сообразуясь с требованиями использующих оценки подсистем и особенностями фактических реализаций исходных сигналов при отсутствии детальных вероятностно-статистических характеристик. Если же сразу ориентироваться на последние, то даже в случае их стационарности остается открытым вопрос: "Как регулярно создавать, по крайней мере, образцовые системы расщепления исходных сигналов в ходе исследовательской идентификации статистических характеристик полезных и помеховых составляющих (компонент)?" Аналогичные соображения высказаны в [17] при рассмотрении противоречивых сторон проблемы "идентификация - регулирование", где предложен и один из теоретических способов построения вероятностных моделей динамических сигналов при изначальном задании лишь пределов изменения уровня и скорости полезной и помеховой компонент.

Отдавая себе отчет в необходимости комплексирования различных подходов с всесторонним выявлением надлежащей роли критериально-ограничительного описания желаемых свойств оценок и остатков, покажем конструктивные возможности выбранного пути синтеза сглаживающих фильтров.

За исходное примем управленческое представление (рисунок 1.1) сглаживающих фильтров как замкнутых следящих[3] САР, функционирующих при наличии флуктуационных и импульсных, аномальных помех [10, 15].

Такое представление фильтров (по аналогии и идентификаторов) способствует взаимообогащению и унификации разработок по оценивающим и регулирующим системам, включая идейное и алгоритмическое содержание МОР-метода, с тесным переплетением названных операций управления, и повышению строгости критериально-ограничительного описания свойств оценок и остатков, начиная с формирования самих ограничений и критериев качества сглаживания динамических сигналов.

Модель [4] полезного сигнала  в роли объекта управления подвержена влиянию регулирующих воздействий – корректировок , которые содержат в общем случае координатные , параметрические и структурные  компоненты. Корректировки  непосредственно изменяют многовариантные (в частности, одновариантные) оценки полезного сигнала и его производных, то есть фазовые координаты модели.

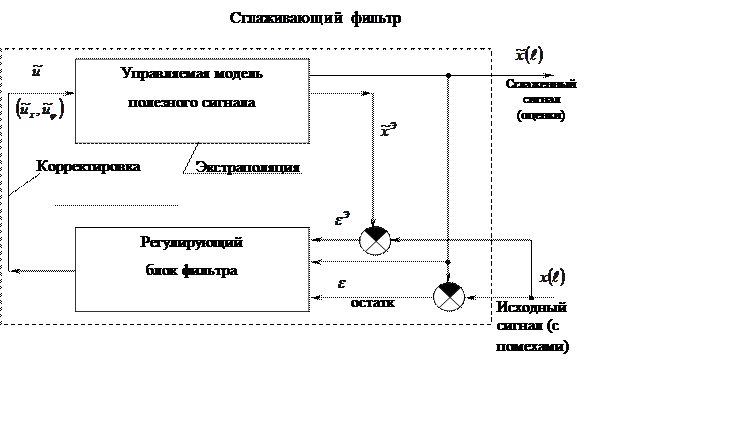Рисунок 1.1 – Принципиальная схема сглаживающего фильтра как следящей САР

С помощью же корректировок  поднастраиваются параметры (коэффициенты) и переключаются структурные звенья управляемой модели полезного сигнала в силу нестационарности обрабатываемых рядов данных, ограничивающих условий и целевых требований. С запуском по опорным значениям x^o в модели формируются и выдаются в динамике результирующие оценки  и вспомогательные оценки . Последние являются выходом экстраполирующих (упреждающих) операций с учетом предыдущих значений  и производных , а возможно, и будущих значений исходного сигнала x или косвенных данных о нем. Для примера в верхнем блоке рисунка 1.2 записаны три варианта линейной модели полезного сигнала.