Структурный анализ в решениях последовательных данных: Учебное пособие (Многовариантная алгоритмизация и применение сглаживающих фильтров. Теоретические основы структурного анализа), страница 19

Второе слагаемое в формуле (2.14) представляет собой нестационарную компоненту.

Для характеристики таких нестационарных случайных процессов предлагается следующая обобщённая структурная функция:

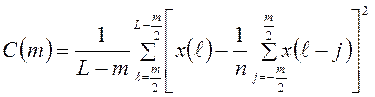.                              (2.15)

Структурная функция обладает инвариантностью относительно квазистационарного характера случайного процесса (а также при смещенности по математическому ожиданию). По своей физической сущности она характеризуем дисперсионные свойства компонент Δх(). График структурной функции строится в координатах «С(m) – m», где m – текущий интервал усреднения.

По аналогии с нормированной корреляционной функцией целесообразно пользоваться нормированной структурной функцией

.                                               (2.16)

В случае конечной выборки структурная функция нормируется делением на дисперсию процесса относительно общего среднего. Вид графика нормированной структурной функции С_Н(m) (рисунок 2.3) позволяет делать предварительные выводы о наличии тренда математического ожидания.

Анализ графиков функции С_H(m) квазистационарного по математическому ожиданию случайного процесса позволяет вскрывать периодические составляющие.

Рисунок 2.3 – Обобщенные структурные функции для

 стационарного (1) и нестационарного (2) по математическому

ожиданию случайных процессов

2.2.2 Разложение сигнала на параллельные составляющие

Функционально однородные составляющие определяются по следующей схеме:

1)  расчёт опорных уровней сигналов;

2)  центрирование регулирующих воздействий относительно своих опорных уровней;

3)  вычисление эффектов регулирующих воздействий;

4)  запоминание эффектов регулирующих воздействий на интервал чистого запаздывания по каждому каналу регулирования;

5)  расчёт приведённого возмущения.

При ретроспективном анализе опорные уровни сигналов можно определять как их средние значения на рассматриваемом отрезке времени, если не происходит резких изменений в условиях работы объекта.

При оперативном определении опорных уровней контролируемых переменных удовлетворительные результаты получаются в случае использования алгоритмов экспоненциального сглаживания.

                ,                                          (2.17)

где х – фактическое значение сигнала в момент времени l;

 х₀ – сглаженное значение, принимаемое за текущий опорный уро- вень;

α – настраиваемый коэффициент.

После резких изменений переменных, не связанных с нарушением технологического режима, необходимо вводить новые начальные условия в виде ожидаемых опорных уровней в алгоритмы экспоненциального сглаживания (2.17).

Идентификация приведённого возмущения предполагает, что динамические характеристики каналов регулирования известны. Описание динамики реальных объектов в приращениях к опорному уровню позволяет с достаточной точностью аппроксимировать вход-выходные зависимости последовательным соединением звена запаздывания и инерционного звена первого порядка.

При моделировании на ЭВМ модели каналов удобно представлять в разностной форме:

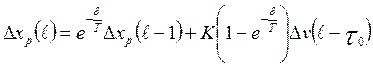.                  (2.18)

Здесь Δх_р – эффект регулирующего воздействия; Δv – отклонение регулируемой переменной от своего опорного уровня v₀; δ – шаг дискретизации;

К – коэффициент передачи объекта; Т – время инерции; τ₀ – чистое запаздывание; l – текущий момент времени.

Приведённое возмущение х_в определяется из соотношения

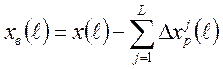,                                   (2.19)

где х – фактическое значение выходной переменной; L – число учитываемых каналов регулирования.

Математическое описание динамики функционально однородных составляющих переменных объекта целесообразно производить путем их дальнейшего расчленения методом динамической компонентной фильтрации, так как применение моделей только стационарных эргодических случайных процессов существенно ограничивает извлечение полезной информации из этих реализаций.