 |
Рисунок 1.2 – Вариант дискретного фильтра
Регулирующий блок фильтра
вырабатывает по алгоритму ![]() координатные
и структурно-параметрические корректировки
координатные
и структурно-параметрические корректировки ![]() взаимодействуя
с управляемой моделью в замкнутых контурах. Для этого служат получаемые им
данные
взаимодействуя
с управляемой моделью в замкнутых контурах. Для этого служат получаемые им
данные ![]() ,
, ![]() ,
,
![]() , которые позволяют находить
различные показатели изменчивости рядов оценок и остатков (экстраполируемых и
фактических). Относительно простые варианты алгоритма fu с настроечными параметрами a, b, r, g1, g2 для контура координатного
регулирования записаны в нижнем блоке рисунка 1.2. Вопросы совместного синтеза
, которые позволяют находить
различные показатели изменчивости рядов оценок и остатков (экстраполируемых и
фактических). Относительно простые варианты алгоритма fu с настроечными параметрами a, b, r, g1, g2 для контура координатного
регулирования записаны в нижнем блоке рисунка 1.2. Вопросы совместного синтеза ![]() и
и ![]() составляют
главный предмет при построении сглаживающих фильтров в рамках рассматриваемой
принципиальной схемы.
составляют
главный предмет при построении сглаживающих фильтров в рамках рассматриваемой
принципиальной схемы.
Управленческая схематизация сглаживающих фильтров при более широком толковании, чем в принятых определениях математической двойственности [18], позволяет ставить и решать задачи инженерного (прикладного) синтеза их на основе объединения разнообразных представлений теории регулирования и теории оценивания, включая принцип временной декомпозиции [13], критерий обобщенной работы [10], меры сложности [14], робастные оценочные функции [19, 20], итерационные структуры следящих систем [12], спектральный анализ [21], новые типы обратных связей [4]. Такого рода методологический комплекс предопределен реальными обстоятельствами, не позволяющими ограничиться однородным математическим методом. Наиболее близкое в этом смысле рассмотрение сглаживающего фильтра как рекуррентного решения детерминированной линейной задачи условной оптимизации квадратичного функционала [19] представляется для инженерного дела первым приближением, полезной эвристикой и составной частью комбинированных способов, но не завершенным для приложений результатом в силу реальной необходимости выбирать усеченные интервалы оптимизации, учитывать импульсные помехи и аномальные данные, вводить ограничения на изменчивость оценок и на сложность алгоритмов, применять гибкие многоструктурные модели и критерии, согласовывать разноцелевые требования и так далее. Именно в таком плане изложен последующий материал с выделением некоторых утверждений, опирающихся на упрощенные аналитические выкладки и, главное, на результаты моделирования, натурных экспериментов и практического внедрения выполненных разработок.
В случае вычленения из
вектора информации одномерных динамических сигналов xj Î x для критериально-ограничительного определения
желаемых свойств сглаживающих оценок xj и получаемых остатков ![]() первоначально применяли
интегральные и дискретные квадратичные критерии
первоначально применяли
интегральные и дискретные квадратичные критерии
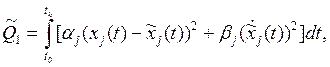 (1.1)
(1.1)
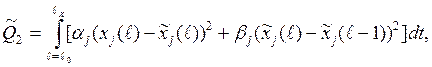 (1.2)
(1.2)
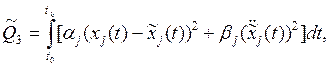 (1.3)
(1.3)
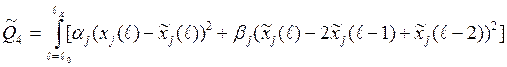 (1.4)
(1.4)
с установлением значений весовых
коэффициентов aj, bj раздельно для каждого варианта (1.1) - (1.4) по методике
[9]. Первое слагаемое характеризует разброс остатков, а второе слагаемое в виде
квадрата первой ![]() или второй
или второй ![]() производных и их дискретных
аналогов характеризует изменчивость (сложность, негладкость) оценок.
Продолжительность участков
производных и их дискретных
аналогов характеризует изменчивость (сложность, негладкость) оценок.
Продолжительность участков ![]() может быть
как фиксированной, так и изменяющейся, в том числе
может быть
как фиксированной, так и изменяющейся, в том числе ![]() ¥,
¥, ![]() ¥. Ограничивающие условия налагаются,
к примеру, заданием значений
¥. Ограничивающие условия налагаются,
к примеру, заданием значений ![]() и пределов
и пределов
![]()
![]() , исходя из конкретных особенностей и
целей сглаживания сигналов (рядов первичных и расчетных данных). В ходе поиска
оценок
, исходя из конкретных особенностей и
целей сглаживания сигналов (рядов первичных и расчетных данных). В ходе поиска
оценок ![]() методом динамического
программирования с условной минимизацией критериев
методом динамического
программирования с условной минимизацией критериев ![]() для
модельных и натурных реализаций xj эмпирически натолкнулись на факт существенно неравномерного
вклада разноудаленных данных в оптимальные оценки, подобный положенным в основу
принципа временной декомпозиции закономерностям инерционных замкнутых систем [13].
Совместно с естественным стремлением к уменьшению запаздываний и инерционности
объектов это побудило к соответствующей интерпретации задачи сглаживания, по
крайней мере, при квадратичных критериях качества с простыми ограничениями[5].
для
модельных и натурных реализаций xj эмпирически натолкнулись на факт существенно неравномерного
вклада разноудаленных данных в оптимальные оценки, подобный положенным в основу
принципа временной декомпозиции закономерностям инерционных замкнутых систем [13].
Совместно с естественным стремлением к уменьшению запаздываний и инерционности
объектов это побудило к соответствующей интерпретации задачи сглаживания, по
крайней мере, при квадратичных критериях качества с простыми ограничениями[5].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.