Ответы на экзаменационные вопросы № 1-69 по дисциплине "Железнодорожные станции и узлы" (Выбор трудного (лёгкого) пути на сортировочной горке. Транспортные узлы, их классификация), страница 5

По кривым t=f(s) устанавливаются: достаточность интервалов t между отцепами для перевода стрелок, шин замедлителей, предельные скорости надвига и др.

Минимальный интервал между бегунами при проходе замедлителя равен:

,

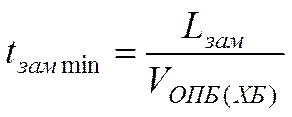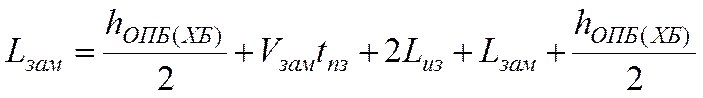, где  – средняя скорость прохода ОХБ (ХБ) на замедлитель, принимается равной 2/3 от максимальной скорости входа на замедлитель; - время на перевод замедлителя в тормозное положение, для КНП -5; - расстояние от конца балки замедлителя до изолирующего стыка  равно 0,5 м; 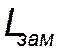 - длина замедлителя по балкам.

Если tзам >= tзам(min), то требуемый интервал достаточен.

Минимальный расчетный интервал между бегунами при проходе стрелочного изолированного участка равен:

,

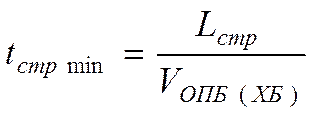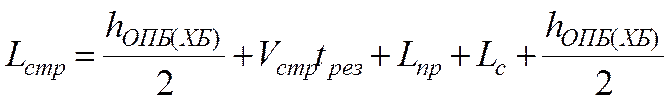, где 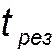- минимальный резерв интервала, равен 1 с; согласно каталога стрелочной продукции для симметричных стрелочных переводов марки 1/6, укладываемых на подгорочных путях.

Если tстр>=tстр(min), то требуемый интервал достаточен.

14.   Классификация расчетных бегунов и их характеристика.

Расчетные бегуны в зависимости от ходовых качеств делятся на очень плохие, плохие, хорошие и очень хорошие. Основным признаком классификации является масса отцепа. К категории очень плохих бегунов относятся вагоны массой порядка 20-25 т, плохим – 30-50 т, хорошим – 50 -70, очень хорошим – 80 -100 т. Выделяют следующие весовые нормы вагонов: Легкая, легкосредняя, средняя, среднетяжелая и тяжелая. Для каждой категории определены значения основного удельного сопротивления, сопротивления от снега и инея.

15.   Построение кривой энергетических высот для ОХБ с частичным торможением

Для проверки работоспособности запроектированной горки, прогнозного расчета её минимальной и максимальной перерабатывающей способности, исследования основных параметров с целью корректировки в сторону улучшения моделируется процесс роспуска вагонов с горки. Самой простой является графическая  модель, позволяющая смоделировать наиболее показательные технологические ситуации роспуска вагонов с горки путем построения кривых скорости и времени хода контрольных отцепов.

Все расчетное расстояние от вершины горки до расчетной точки разбивается на четыре участка: ВГ – начало I ТП; начало I ТП – начало II ТП; начало II ТП – начало III ТП; начало III ТП – расчетная точка.  В каждом промежутке определяется сумма w0 и wсв и рас-ся энергетическая высота:

.

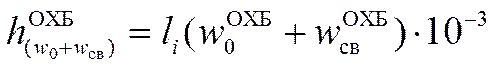На третьем и четвертом участках горки при неблагоприятных условиях скатывания к основному удельному сопротивлению и дополнительному от среды и ветра добавляется удельное сопротивление от снега и инея:

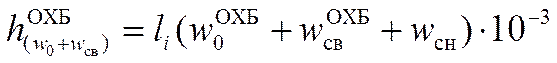
Полученные величины 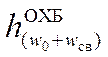откладываются вниз по перпендикуляру от линии МN в конце границ участков нарастающим  итогом. Построенные точки соединяются прямыми отрезками. Полученная линия будет линией энергетических высот, потерянных ОХБ на преодоление основного и дополнительного сопротивлений от среды и ветра.

Для получения кривой энергетических высот, потерянных отцепом на преодоление всех сил сопротивления, геометрически складываются соответствующие ординаты построенных линий.

Вниз от линии 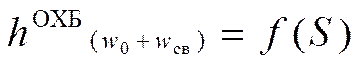откладываются по перпендикулярам, опущенным из точек переломов, ординаты  ломаной .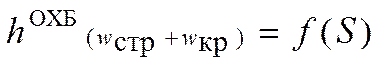

При построении кривой 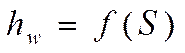, соответствующей частичному торможению для проверки профиля горки установлены наиболее трудные условия: разделение отцепов на последней стрелке пучка и обеспечение интервалов между отцепами на первой разделительной стрелке и тормозных позициях, достаточных для перевода остряков и шин замедлителей из нетормозного положения в тормозное. Эти условия выполняются наилучшим образом при равенстве средних скоростей ОПБ и ОХБ на отрезке пути о ВГ до разделительной стрелки. Из-за значительного различия в ходовых качествах ОПБ и ОХБ  и возможности торможения только  на ограниченных участках обеспечить равенство их скоростей во всех точках невозможно. Поэтому в основу алгоритма решения  положено  примерное равенство средних скоростей скатывания отцепов.   При 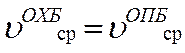интервал на разделительной стрелке будет примерно равен интервалу на вершине горки, что достаточно  для гарантированного перевода стрелки. Графически можно получить такое решение, приближая кривую с частичным торможением  к кривой  за счет варьирования степени торможения на позициях.