Навчально-методичний посібник для організації самостійної та індивідуальної роботи з дисципліни "Вища математика" (частина І), страница 9

4.  Аналіз маргінальної продуктивності.

5.  Еластичність попиту і пропозицій, виробничих функцій і т.п.

6.  Виробничі функції кількох змінних і граничний аналіз.

7.  Частинні граничні витрати, дохід і прибуток.

8.  Максимізація прибутку і мінімізація витрат.

9.  Частинні еластичності функції та їх економічна інтерпретація.

Результат виконання роботи: конспект, виконання домашнього завдання.

Форма контролю: перевірка конспекту,усне опитування, обговорення питань, тестування.

Глава ІІ.МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО ПРАКТИЧНИХ ЗАНЯТЬ З ДИСЦИПЛІНИ «ВИЩА МАТЕМАТИКА»

МОДУЛЬ 1

Розділ 2. ЕЛЕМЕНТИ ТЕОРІЇ МАТРИЦЬ І ВИЗНАЧНИКИ

Основні питання, що виносяться на практичні заняття за розділом 2:

1.  Дії з матрицями.

2.  Обчислення визначників різними способами.

3.  Знаходження оберненої матриці.

Після опрацювання розділу на практичних заняттях студент повинен

знати: базові поняття і положення лінійної алгебри (матриця, види матриць, дії з матрицями; визначники, їх властивості та способи їх обчислення);

вміти: виконувати дії з матрицями, обчислювати мінор та алгебраїчне доповнення елементів квадратної матриці, обчислювати визначник різними способами, в тому числі, з використанням його властивостей, знаходити обернену матрицю.

Рекомендована література:

[1], т. І, с. 73-89.

[2], с.  82-128.

[3], с. 13-30.

Рекомендації до розв’язання типових прикладів розділу 2

2.1. На випуск одиниці двох видів продукції А₁, А₂ витрачаються комплектуючі В₁, В₂, В₃, В₄  у кількостях, що задаються матрицею

.

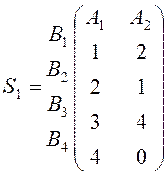У свою чергу, на складання одиниці  виробів В₁, В₂, В₃, В₄ витрачається продукція С₁, С₂, С₃, задана матрицею

.

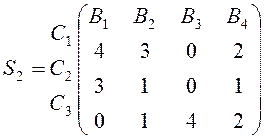Визначити потрібну кількість елементів D₁,D₂, D₃  вихідного матеріалу, коли відомо, що витрати їх на одиницю С₁, С₂, С₃  задано матрицею

.

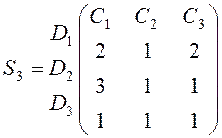Матрицею витрат елементів D₁, D₂,D₃  на одиницю кінцевої продукції А₁  та А₂ можна подати у вигляді добутку матриць K=S₃·S₂·S₁,  тобто

.

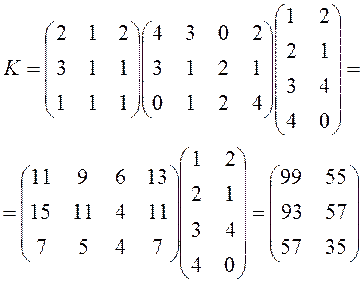Знаючи виробничу програму випуску кінцевої продукції, можна визначити потрібну кількість вихідного матеріалу. Наприклад, якщо треба випустити готову продукцію А₁=50, а А₂=100 одиниць, то для цього матрицю Kмножимо на вектор 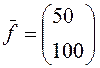 . Отже,

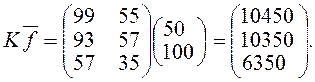
2.2. Три фірми випускають4 види виробів. Задано матриці випуску продукції в липні і серпні:

,

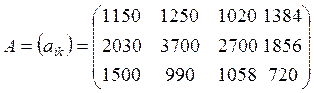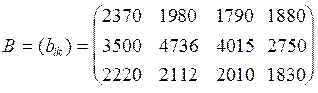
де а_iкі b_ik (i = 1, 2, 3; k = 1, 2, 3, 4) - накопичений з початку року на кінець деякого місяця обсяг продажу виробів відповідного виду по одній фірмі. Знайти обсяг продажу виробів за місяць на кожній фірмі.

Розв’язання:

Обсяг продажу продукції на кожній фірмі за місяць:

C = B – A

Відповідь: місячний обсяг продажу виробів на кожній фірмі .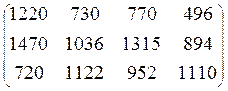

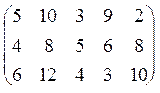
2.3. Підприємство випускає три види продукції, що характеризуються матрицей ‑  планом Х = ( 1074 ). При випуску продукції використовують 5 типів сировини. Задано матрицю витрат сировини: A = (a_ik) = , де a_ik ‑ витрати сировини на одну одиницю продукції визначеного виду (к ‑ тип сировини, i ‑ вид продукції). Матриця

S =  задає вартість однієї одиниці кожного виду сировини. Визначити: а) необхідну кількість одиниць сировини кожного виду для забезпечення плану; б) вартість сировини для одиниці кожного виду продукції; в) загальну вартість сировини при виконанні плану випуску Х.

Розв’язання:

a) Знайдемо необхідну кількість одиниць сировини кожного виду для забезпечення плану

С = Х А = =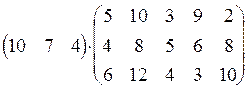

б) Знайдемо вартість сировини для одиниці кожного виду продукції

D = S A =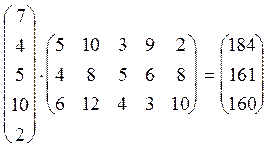

в) Знайдемо загальну вартість сировини при виконанні плану випуску Х

 F = X D = .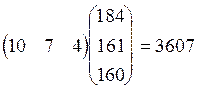

2.4. Виконати розрахунок заробітної плати, що припадає на кожне замовлення при виробництві різноманітних виробів, користуючись даними таких таблиць:

Виріб	Витрати робочого часу на кожному з робочих місць
	1	2	3	4
А	0.8	2.1	1.2	3.0
В	1.3	0.5	2.8	0.2
С	1.1	1.0	2.5	1.8