12) Теорема Кронекера-Капеллі.
13) Методи Гаусса і Жордана-Гаусса розв’язування системи рівнянь.
14) Загальний і базисний розв’язки системи рівнянь.
15) Лінійна однорідна система рівнянь, фундаментальна система її розв’язків та структура загального розв’язку.
16) Метод оберненої матриці розв'язування системи рівнянь.
Результат виконання роботи: складання конспекту, виконання домашнього завдання.
Форма контролю: усне опитування, обговорення питань, тестування, контрольна робота за модулем 1, складання, аналіз та обговорення практико-орієнтованих задач.
Розділ 4. ЕЛЕМЕНТИ МАТРИЧНОГО АНАЛІЗУ
Тема 1.7. Застосування матриць і системи лінійних алгебраїчних рівнянь в економічному аналізі
1. Застосування матриць і систем рівнянь для аналізу обсягів випуску продукції, аналізу прибутковості–збитковості.
2. Міжгалузеві виробничі зв’язки.
3. Матриці виробничих витрат.
4. Модель міжгалузевого балансу (модель В.Леонтьєва).
5. Власні числа і власні вектори матриці та їх застосування у лінійному обміні (міжнародна модель торгівлі).
6. Поняття квадратичної форми та її запис у матричному вигляді.
7. Канонічна форма квадратичної форми.
8. Умови знаковизначеності квадратичної форми.
Література:
[1], т. І, с. 121-123.
[2], с. 153-180,192-197.
[3], с. 65-81.
Задачі, рекомендовані до розв’язання:
[3], с.79, № 1.87.
Питання для самоконтролю
1. Власні числа і власні вектори матриці та їх застосування у лінійному обміні (міжнародна модель торгівлі).
2. Поняття квадратичної форми та її запис у матричному вигляді.
3. Канонічна форма квадратичної форми.
4. Умови знаковизначеності квадратичної форми.
Результат виконання роботи: конспект, виконання домашнього завдання.
Форма контролю: перевірка конспекту,усне опитування, обговорення питань, тестування, контрольна робота за модулем 1, складання, аналіз та обговорення практико-орієнтованих задач.
Розділ 5. ЕЛЕМЕНТИ ВЕКТОРНОЇ АЛГЕБРИ ТА АНАЛІТИЧНОЇ ГЕОМЕТРІЇ
Тема 1.8. Вектори на площині і в просторі та дії з ними. n-вимірний векторний простір
1. Поняття вектора на площині і в просторі.
2. Геометричне додавання, віднімання векторів та множення вектора на скаляр.
3. Проекція вектора на вісь.
4. Координати вектора і запис його через орти.
5. Довжина і напрямні косинуси вектора.
6. Скалярний добуток векторів і кут між векторами.
7. Властивості скалярного добутку векторів.
8. Умови паралельності і перпендикулярності векторів.
9. Векторний добуток векторів та його властивості.
10.Знаходження координат векторного добутку за координатами співмножників.
11.Мішаний добуток векторів та його геометричне тлумачення.
12.Поняття n-вимірного векторного простору та його базису.
Література:
[1], т. І, с. 125-139.
[2], с. 227-238.
[3], с. 82-115.
Задачі, рекомендовані до розв’язання:
[3], с.114, № 2.30-2.44.
Питання для самоконтролю
1. Що таке вектор? Які вектори є рівними?
2. Як знайти суму і різницю двох векторів?
3. Що є вектором, помноженим на скаляр?
4. Якими властивостями володіють операції складання векторів і множення векторів на скаляр?
5. Що таке координати вектора? Як знайти координати вектора по координатах його початку і кінця?
6. Дати визначення скалярного добутку.
7. Яка необхідна і достатня умова перпендикулярності векторів?
8. Перерахувати властивості скалярного добутку.
9.
Як обчислити 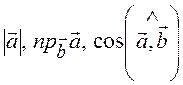 ?
?
10.Чому рівний скалярний добуток векторів, розкладених по ортам? Модуль вектора?
11.Як
знайти одиничний вектор, сонаправлений з ![]() ?
?
12.Дати визначення векторного добутку.
13. Дати визначення змішаного добутку.
14.Два вектори називаються колінеарними, якщо….
15.Три вектори називаються компланарними, якщо…..
16.Ортом
вектора ![]() називається
називається
17.Добутком
вектора ![]() на число х називається
на число х називається
18.Різницею
![]() двох векторів називається
двох векторів називається
19.Що називається координатами вектора?
20.Що можна сказати про координати рівних векторів?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.