Навчально-методичний посібник для організації самостійної та індивідуальної роботи з дисципліни "Вища математика" (частина І), страница 18

Використовуючи рівняння прямої, що проходить через точки А і М, знаходимо рівняння медіани АМ: 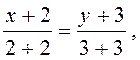   звідки 3х-2у=0.

5.11. Провести серединний перпендикуляр відрізка АВ, де А(0; -2), В(4; 0).

Розв’язання.

 

Маємо С(2; -1). Розглядаючи  як вектор нормалі шуканої прямої, маємо: 4(х-2) +2(у+1) =0, звідки 2х + у –2 =0.

5.12. Дані рівняння сторін трикутника:

х + 3у –7= 0 (АВ), 4х –у- 2= 0 (ВС),6х +8у –35= 0 (АС).

Знайти довжину висоти, проведеної з вершини В.

Розв’язання.

Визначимо координати точки В. Розв’язуючи систему рівнянь

х + 3у –7= 0 та  4х –у- 2= 0, одержимо х=1,у= 2, тобто В(1;2). Скористаємося формулою для обчислення відстані від точки М₀( х₀;у₀)до прямої Ах +Ву + С =0:

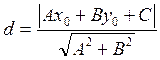
Знаходимо довжину висоти ВВ₁ як відстань від точки В до прямої АС:

 

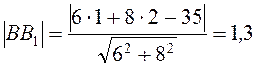
5.13.Знайти проекцію точки Р(4;9)на пряму, що проходить через точки А(3; 1) та В(5; 4).

Розв’язання. Проекція точки на пряму- це основа перпендикуляра, опущеного з точки на пряму. Для її одержання достатньо розв”язати сумісно рівняння прямої АВ і прямої, що проходить через точку Р перпендикулярно АВ.

Рівняння АВ запишемо, скориставшись рівнянням

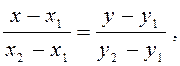   де  та - відомі точки прямої.

Тоді 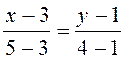      або  .

Рівняння другої прямої запишемо, скориставшись рівнянням

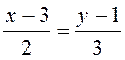  де - вектор нормалі прямої, а

- точка прямої.

Вибравши в якості нормального вектора напрямний вектор  прямої АВ, маємо:

2(х-4) +3(у-9)=0.

Таким чином:

        

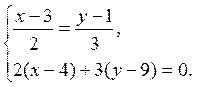
Розв’язавши цю систему, одержимо: х = 7, у = 7.

Отже, проекція точки Р на задану пряму - точка С(7, 7).

5.14.Валова продукція на 1 га сільскогосподарського угіддя за 4 роки збільшилась на 24,4%. Скласти рівняння прямої, яке відображає зміну валової продукції на 1 га протягом чотирьох років за умови, що валова продукція у відсотках змінюється пропорційно часу.

Розв’язання. Валову продукцію, вироблену в перший рік, приймемо за 100% і будемо шукати рівняння прямої у вигляді y=kx+b:

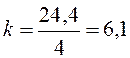;   100=6,1·1+b;                 b=93,9.

Отже, y=6,1x +93,9             (x – рік).

5.15. Перевезення вантажу від даного міста в перший пункт, що знаходиться на відстані 100 км коштує 200 гр. од., а в інший, що знаходиться на відстані 400 км - 350 гр. од.   Встановити залежність вартості перевезення y  від відстані x, якщо вартість є лінійна функція від відстані (якість доріг не враховується).

Розв’язання:

Залежність вартості перевезення від відстані виражається лінійною функцією 

 y = k·x + b

 ;

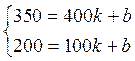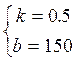
Таким чином,  y = 0,5x + 150

Відповідь:залежність вартості перевезення від відстані y(x) виражається функцією y = 0,5x + 150.

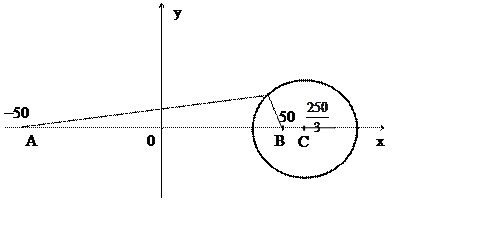
5.16. Два підприємства, розташовані одне від іншого на відстані 100 км, виробляють однакову продукцію, причому ціна реалізації одиниці продукції на обох підприємствах однакова і складає Р центів. Нехай транспортні витрати на перевезення одиниці продукції від підприємства А до споживача складають 1 цент/км, а від підприємства В – 2 центи/км (див. рисунок.). Для яких споживачів витрати на придбання одиниці виробу підприємств А і В будуть однаковими? Як доцільніше прикріпити споживачів до підприємств?

Розв’язання. Складемо математичну модель задачі.

Проведемо через точки А і В на площині пряму і приймемо її за вісь Ох, вісь ординат проведемо через середину відрізка [АВ]. Нехай споживач знаходиться в точці М (х, у), позначимо АМ = S₁, BM = S₂.

Витрати споживача на придбання одиниці продукції у підприємств А і В складуть, відповідно, P+S₁ і P+2S₂ центів. Витрати споживача однакові, якщо P+S₁=P+2S₂ чи S₁=2S₂, тобто

.                            (1)

 

Витрати споживача менше при придбанні продукції на підприємстві В, якщо S₁>2S₂, тобто

                       (2)

Відповідно витрати будуть менше на підприємстві А, якщо S₁<2 S₂, тобто

 .                    (3)

Складена така математична модель задачі: координати яких точок на площині задовольняють: а) рівнянню (1); б) нерівності (2); в) нерівності (3)?

Для розв’язання цієї задачі спростимо рівняння (1):

  

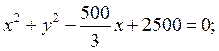
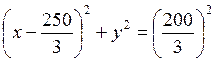                                      (1’)