Навчально-методичний посібник для організації самостійної та індивідуальної роботи з дисципліни "Вища математика" (частина І), страница 10

Замовлення	Кількість виробів				Робоче місце	Годинна заробітна плата
	A	B	C		1	1.30
K	5	7	3		2	1.25
L	4	0	2		3	1.40
M	6	2	1		4	1.45

 Розв’язання:

Визначимо матриці: Q - кількість виробів, P – витрати  робочого часу на кожне з робочих місць, J - годинна зарплата:

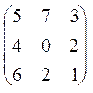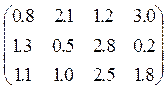Q = , P =  , J = ,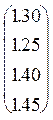

і виконаємо розрахунок зарплати

(Q× P) × J =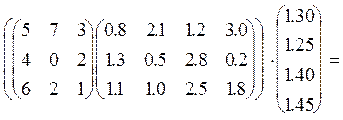

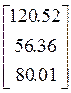
Відповідь: нарахування заробітної плати на замовлення K – 120, 52 гр.од., на замовлення L – 56,36 гр.од.; на замовлення M – 80, 01 гр.од.

2.5. Обчислити визначник

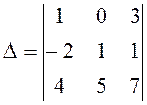
а) за правилом трикутника:

 = 1 · 1 · 7 + 0 · 1 · 4 + (-2) · 5  · 3 – 4 · 3  ·1 – 7 · (-2)  · 0 – 1 ·1  · 5 =  - 40 ;

б) розкладанням за елементами першого рядка:

а₁₁ = 1;     А₁₁  =  (-1)¹⁺¹ · 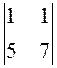    = 1· (7 – 5) = 2 ;

а₁₂ = 0;   а₁₃ = 3,  А₁₃  =  (-1)¹⁺¹ · 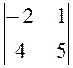    = 1· (-10 – 4) = -14 ;

 = 1 · 2 + 0 + 3 · (-14) = - 40.

2.6. Знайти обернену матрицю до матриці

.

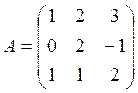Для визначника третього порядку знаки алгебраїчних доповнень будуть такими:

.

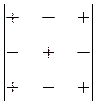Виконаємо необхідні обчислення для відшукання оберненої матриці. Спочатку обчислимо її визначник, щоб переконатися, що обернена матриця існує:

detA=4–2–6+1= –3.

Враховуючи чергування знаків в алгебраїчних доповненнях, дістанемо

                      

               

           

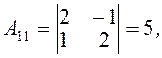
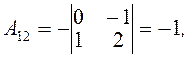
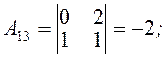
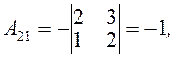
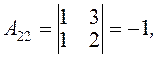
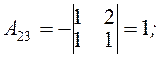
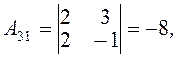
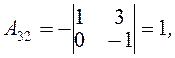
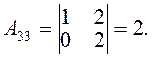
Отже, матриця, обернена до матриці A, має такий вигляд:

.

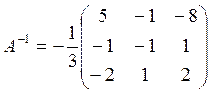Правильність знайденої оберненої матриці перевіряємо множенням матриці Aна обернену ліворуч або праворуч:

.

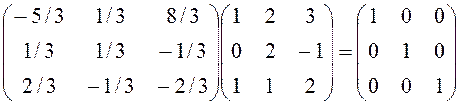Задачі, рекомендовані до розв’язання на практичних заняттях з розділу 2

1. Дано матриці:

.

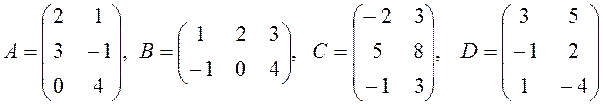Чи можна скласти матрицю А з матрицею В? Матрицю А з матрицею С.

Знайти А+ С; 2 А-3С+D.

2. Підприємство виробляє продукцію трьох видів і використовує сировину двох типів. Норми витрат сировини на одиницю продукції кожного виду задані матрицею 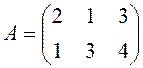. Вартість одиниці сировини кожного типа задана матрицею В=(10       15). Які загальні витрати підприємства на виробництво 100 одиниць продукції першого вигляду, 200 одиниць продукції другого вигляду і 150 одиниць продукції третього вигляду.

3. У даній таблиці зазначена кількість одиниць продукції, що відвантажується щодня на фабриках 1, 2 і 3 у пункти призначення А, В та  С:

	Пункт призначення
Фабрика	А	B	C
1	9	20	7
2	8	10	15
3	2	21	11
Витрати на перевезення	1700	1950	1880

Знайти матрицю доставки одиниці продукції з кожної фабрики в кожний пункт.

4. Намічено випустити на продаж у декілька магазинів комп'ютерів чотирьох типів. Знайти загальну вартість комп'ютерів по кожному з типів, якщо вартість усіх комп'ютерів по трьох магазинах А, В та С дорівнює відповідно 3980, 1870, 3530 гр.од. Вартість комп'ютера кожного типу в кожному магазині (гр. од.) приведена в таблиці:

Тип комп'ютера	Магазин
	А	B	C
1	22	34	30
2	20	15	17
3	35	30	12

5. Два заводи випускають вироби M, N, P вищої, першої і другої категорії якості. Кількість випущених кожним заводом виробів по кожній категорії якості характеризується такою таблицею:

Який випуск виробів по зазначених категоріях якості?