Навчально-методичний посібник для організації самостійної та індивідуальної роботи з дисципліни "Вища математика" (частина І), страница 30

Варіант 27. Знайти похідну:

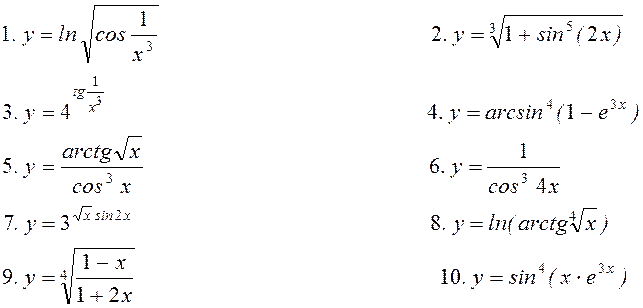
11. Знайти частинні похідні для функцій

;

.

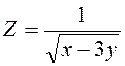12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (2;4), (3; 1)

Варіант 28. Знайти похідну:

 

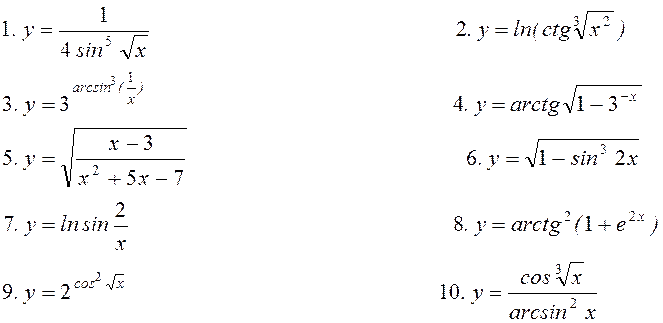
11. Знайти частинні похідні для функцій

;

.

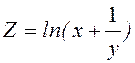12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (3;1), (-1; 1)

Варіант 29. Знайти похідну:

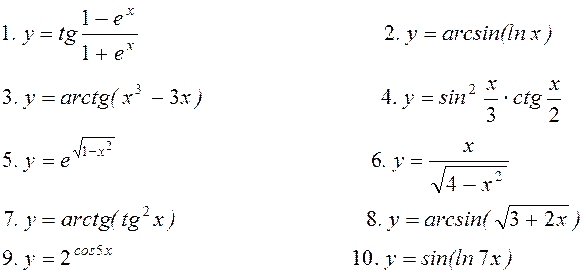
11. Знайти частинні похідні для функцій

;

.

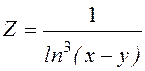12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (1;-2), (6; -8)

Варіант 30. Знайти похідну:

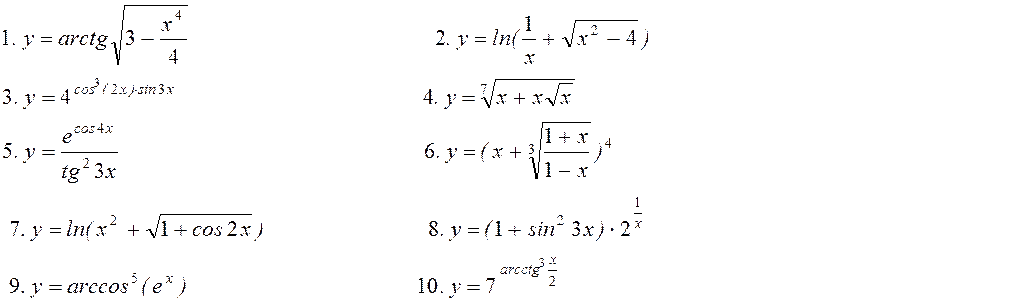11. Знайти частинні похідні для функцій

;

.

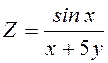12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (1;-1), (1; -3)

Глава ІV. МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО ВИКОНАННЯ МОДУЛЬНИХ КОНТРОЛЬНИХ РОБІТ З ДИСЦИПЛІНИ «ВИЩА МАТЕМАТИКА»

Типовий варіант до модульної контрольної роботи №1.1

1) Розв`язати систему лінійних рівнянь методами Крамера, Гаусса, Жордана-Гаусса та матричним методом.

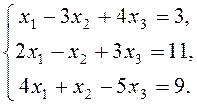
2) Дослідити систему на сумісність.

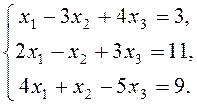
3) Розв¢язати систему:

х₁ + 2х₂ +3х₃ +4х₄ = 11

2х₁ + 3х₂ +4х₃ + х₄  = 12

3х₁ + 4х₂ + х₃ +2х₄  = 13

4х₁ +  х₂ +2х₃ +3х₄  = 14

Критерії оцінювання

Контрольне завдання складається з таких завдань:

№ 1: розв¢язати дану систему лінійних рівнянь чотирма способами – за правилом Крамера, матричним методом, методом Гаусса, методом Жордана-Гаусса. При застосуванні правила Крамера визначники обчислювати різними способами;

№ 2: дослідити дану систему лінійних рівнянь на сумісність; визначити тип системи (визначена, невизначена, несумісна). Кожне з п¢яти завдань оцінюється максимально в 1 бал. Останнє завдання – додаткове.

Типовий варіант до модульної контрольної роботи №1.2

1.1.

Знайти 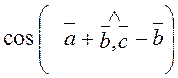, орт вектора     

2. А(0,4,0) , В(-1,-3,2) ,С(-4,-1,2) , D(4,-3,-1)

Знайти , проекцію вектора  на  .

3. Довести, що дані вектори утворюють базис та розкласти вектор  за цим базисом:

    .

4. Знайти рівняння прямої на площині, що проходить через точку А(4,-3) перпендикулярно вектору .

5. Знайти рівняння прямої на площині, яка проходить через точки А(2,-6) і В(3,0).

6. Скласти рівняння прямої, яка проходить через точку А(2,4,-7) паралельно осі ОУ.

7. Скласти рівняння площини, яка проходить через точку М_о (1,-1,4) паралельно площині х – у + 3z – 1=0.

8. Знайти точку перетину прямої і площини

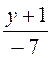= =        і  6х -3у+ z –1= 0

Критерії оцінювання

– кожна задача оцінюються максимально по 1 балу; ці задачі передбачають використання основних формул, фактів, положень векторної алгебри (задачі на знаходження довжини вектора, орта вектора, кута між векторами, проекції вектора на вектор, використання умов ортогональності або колінеарності двох векторів) та аналітичної геометрії на площині та у просторі (використання різних видів рівнянь прямої та площини, знаходження кутів між двома прямими, між двома площинами, між прямою та площиною, знаходження відстані від точки до прямої, від точки до площини, різні випадки взаємного розташування прямих та площин.

Типовий варіант до модульної контрольної роботи №2.1

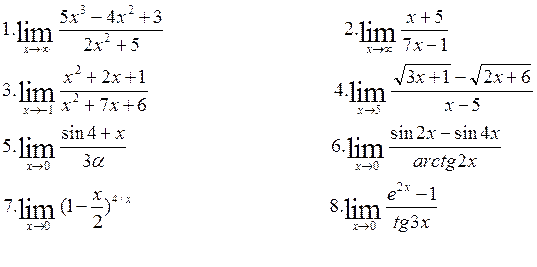
9.Дослідити на неперервність, визначити точки розриву, якщо вони існують:

.

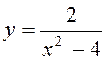10. Дослідити на неперервність, визначити точки розриву, якщо вони існують:

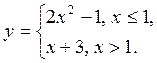
Критерії оцінювання

Контрольне завдання складається з таких завдань:  знайти границі функції у завданнях  №1-№8, дослідити на неперервність, визначити точки розриву, якщо вони існують, у завданнях №9 та №10. Кожне з десяти завдань оцінюється максимально в 1 бал.

Типовий варіант до модульної контрольної роботи №2.2

1.Обчислити похідні функцій:  y = arcsin ,   ,   .

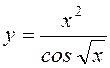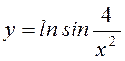2. Знайти похідні неявних функцій:  x² + xy + y² = 6;   .

3. Знайти похідну функції методом логарифмічного диференціювання:

4. Записати рівняння дотичної до даної кривої в точці з абсцисою х₀:

.

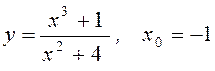5. Знайти диференціал функції двох змінних

6. Знайти градієнт функції в т. А та похідну в цій точці за напрямом вектора :

, т. A (1;3), (1; -1).

7. Обчислити границю функції, використовуючи правило Лопіталя:  .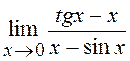

Критерії оцінювання