Навчально-методичний посібник для організації самостійної та індивідуальної роботи з дисципліни "Вища математика" (частина І), страница 19

Рівняння (1’) визначає коло з центром у точці 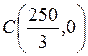 радіуса . Тому споживачам, які знаходяться на колі , усе рівно, де робити закупівлю (в А чи в В).

Аналогічно нерівності (2) рівносильно нерівності

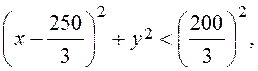                               (2’)

яке визначає внутрішність кола. Тому для покупця, що знаходиться усередині кола, вигідніше купувати продукцію на підприємстві В.

Так само нерівність (3) переходить у нерівність

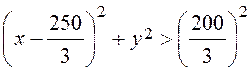,                               (3’)

де (3') означає зовнішність кола. Тому якщо покупець знаходитися поза колом, то йому вигідніше робити закупівлі на підприємстві А.

5.17. Відстань від залізничної станції, що відправляє споживачам готову продукцію, до кар'єру, що забезпечує сировиною підприємство, дорівнює 20 км.  Відомо, що підприємство знаходиться в два рази ближче від джерела сировини, чим від станції - відправника готової продукції. Знайти рівняння множини всіх можливих місць розташування підприємства, прийнявши за вісь абсцис пряму, що проходить через точки, які відповідають кар'єру і залізничній станції; початок координат узяти по середині між цими точками.

Розв’язання

Складемо рівняння 2S₁ = S₂, де S₁ - відстань від підприємства до джерела сировини, а S2 - до станції  

Збудуємо в квадрат обидві частини рівняння і приведем подобные

3x² + 100x + 3y² + 300 = 0

x² + x + y² + 100 = 0

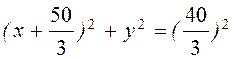
Отже, множиною всіх можливих місць розташування підприємства є коло з центром в точці (-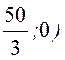 та радіусом .

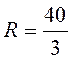5.18.Скласти рівняння площини, яка проходить через точку М₀(2;3;5) і перпендикулярно вектору  .

Розв’язання.

 

Достатньо скористатися рівнянням площини, яка проходить через дану точку М₀(x₀;y₀;z₀)  і має вектор нормалі :

.

Тоді у нашому випадку маємо:

4(х-2)+3(у-3)+2(z-5)=0, звідси одержуємо рівняння шуканої площини:

4х +3у +2z –27 =0.

5.19. Написати рівняння площини, що проходить через точку М₀(2; 3; -1) паралельно площині 5х – у + 3z = 5.

Розв’язання.

Скориставшись рівнянням площини, що проходить через задану точку, запишемо А(х-2)+В(у-3)+С(z+1)=0. З паралельності площин випливає, що шукана площина має нормальний вектор

, тому рівняння шуканої площини має вигляд

5(х-2) –(у-3) +3(z+1) = 0, або 5х – у + 3z – 4 = 0.

5.20. З точки Р(2;3;-5) на координатні площини опущені перпендикуляри. Скласти рівняння площини, що проходить через їх основи.

Розв’язання. Основами перпендикулярів, опущених на координатні площини, служать такі точки: М₁(2;3;0), М₂(2;0;-5), М₃(0;3;-5).Застосуємо рівняння площини, що проходить через три точки  , які не належать одній прямій:

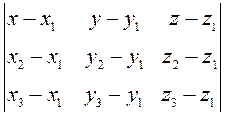=0

Тоді маємо:

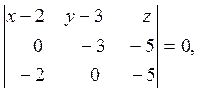  або 15х +10у –6z-60=0.

5.21. Скласти рівняння площини, яка проходить через початок координат перпендикулярно прямій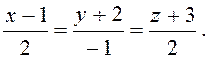   

Розв’язання.

З умови задачі випливає, що напрямний вектор прямої

є вектором нормалі для шуканої площини.

Тоді, аналогічно попередній задачі, маємо:

2(x-0) –1(y-0) +2(z-0)=0, звідки  2x –y + 2z =0.

5.22.Скласти рівняння прямої, яка проходить через точку М(5; 3; 4) і паралельна вектору .

Розв’язання.

Скористаємося канонічним рівнянням прямої, яка проходить через точку М₀(x₀; y₀; z₀) та має напрямний вектор .

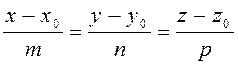
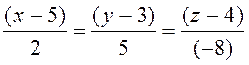
5.23. Написати канонічні і параметричні рівняння прямої, що проходить через точку М₀(1; -2; 2) паралельно осі ОУ.

Розв’язання.Вектор  розташований на осі ОУ , за умовою паралельний прямій. Тому його можна вважати напрямним вектором цієї прямої, звідки одержуємо, що канонічні рівняння прямої мають вигляд:

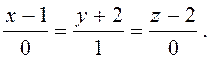
При переході до параметричних рівнянь треба врахувати, що нулі в знаменниках 1-го та 3-го відношень означають, що

х –1 =0 та z –2 =0. Прирівнюючи 2-е відношення до t, одержимо: y =-2 + t.

Отже, шукані параметричні рівняння мають вид х =1, у =-2+ t, z =2.

5.24.Скласти рівняння прямої, що проходить через точку А(2; 4; -6) та середину В відрізка, кінцями якого є точка С(2; 0; -4) та точка D, симетрична точці А відносно початку координат.

Розв’язання. Маємо точку D(-2; -4; 6), тоді з формул для обчислення координат середини відрізка одержуємо точку В(0; -2; 1). Скористаємося канонічним рівнянням прямої, яка проходить через точки А(x₁; y₁; z₁) B(x₂; y₂; z₂):