Контрольне завдання складається з 10 завдань: обчислити похідну, знайти
похідну неявної функції, знайти похідну функції методом логарифмічного
диференціювання, записати рівняння дотичної до даної кривої в точці з абсцисою х0,
знайти диференціал функції двох змінних, знайти градієнт функції в т. Ата похідну за напрямом вектора ![]() , обчислити
границю функціі, використовуючи правило Лопіталя. Кожний з десяти прикладів
оцінюється максимально в 1 бал.
, обчислити
границю функціі, використовуючи правило Лопіталя. Кожний з десяти прикладів
оцінюється максимально в 1 бал.
Глава V. ІНДИВІДУАЛЬНЕ ДОМАШНЄ ЗАВДАННЯ №1
З ДИСЦИПЛІНИ «ВИЩА МАТЕМАТИКА» ДЛЯ СТУДЕНТІВ ЗАОЧНОЇ ФОРМИ НАВЧАННЯ ТА РЕКОМЕНДАЦІЇ ДО ЙОГО ВИКОНАННЯ
Індивідуальна робота містить завдання за розділами дисципліни: ЕЛЕМЕНТИ ТЕОРІЇ МАТРИЦЬ І ВИЗНАЧНИКИ, ЗАГАЛЬНА ТЕОРІЯ СИСТЕМ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ, ЕЛЕМЕНТИ ВЕКТОРНОЇ АЛГЕБРИ ТА АНАЛІТИЧНОЇ ГЕОМЕТРІЇ, ЕЛЕМЕНТИ ТЕОРІЇ ГРАНИЦЬ, ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ.
Необхідно с самого початку вірно встановити свій варіант (від 1 до 10), який відповідає останній цифрі номера за журналом групи.
Основні вимоги до виконання індивідуального завдання:
самостійність виконання;
своєчасність виконання роботи;
відповідність номеру варіанта, в противному разі робота буде повернена на повторне виконання;
робота повинна бути виконана повністю;
завдання треба розташовувати по порядку за номерами, що вказані в завданні, із зберіганням нумерації;
кожне завдання необхідно оформити за такою схемою: умова завдання (переписати у відповідності до свого варіанту); розв’язання задач (має бути обґрунтованим, з наведенням формул, назв відповідних теорем, відомих фактів, якими користувалися); відповідь (повна);
роботу треба виконати в окремому зошиті з полями для зауважень викладача, інтервалами між строками, без скорочень, розбірливим почерком;
наприкінці роботи наводиться список літератури, ставиться дата її виконання, підпис студента, залишається місце для рецензії.
Перед виконанням завдань необхідно детально вивчити методичні вказівки (див. §§ 3-9 цієї глави), які містять стислий виклад основних теоретичних відомостей, формули, алгоритми, рекомендовані приклади, посилання на літературу і мають метою допомогти студенту самостійно оволодіти матеріалом і навичками розв’язання задач.
Якщо в роботі припущені помилки, не всі відповіді розкривають зміст питань, вона не зараховується і повертається студентові для доопрацювання (в тому ж зошиті). Роботи, що виконані несамостійно, неохайно, нерозбірливим почерком, а також не за встановленим варіантом, повертаються без перевірки.
§2. ЗАВДАННЯ ІНДИВІДУАЛЬНОЇ РОБОТИ
(N– номер варіанта (від 1 до 10), відповідає останній цифрі номера за журналом)
Завдання № 1. Розв’язати систему лінійних рівнянь 1) за правилом Крамера, 2) матричним методом, 3) методом Гаусса, 4) методом Жордана-Гаусса:
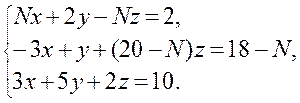
Завдання № 2. Дані точки А(N; 3; -1); В(7; 0; 1), С(2; -N; 4),D(4; 2; 5). Знайти:
1) довжину векторів ![]() ; 2) орт
вектора
; 2) орт
вектора ![]() 3) кут
між векторами
3) кут
між векторами ![]() та
та ![]() .
.
Завдання № 3. Дані точки: А(N-3; 1), В(1; N-6;), С(N-10; 2). Скласти рівняння:
1) прямої АВ; 2) висоти трикутника АВС, що проходить через вершину В; 3) прямої, що проходить через точку С паралельно прямій АВ.
Завдання № 4. Дано: М1(n;
3; -1), М2(2; n; 4), М3(5; -2; 3), 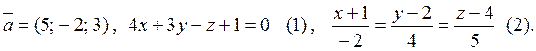
1) Скласти рівняння площини:
1) що проходить
через точку М1 перпендикулярно вектору ![]() ;
;
2) що проходить через точку М1 паралельно площині (1);
3) що проходить через точку М3 перпендикулярно прямій (2).
2) Скласти рівняння прямої у просторі:
1) що проходить через точку М2
паралельно вектору ![]()
2) що проходить через точку М3 паралельно прямій (2);
3) що проходить через точки М1 та М2;
4) що проходить через точку М3 перпендикулярно площині (1).
Завдання № 5. Обчислити границі функцій:
1) 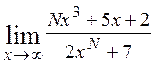 , 2)
, 2) 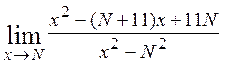 , 3)
, 3) 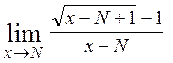 ,
,
4) 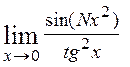 , 5)
, 5) 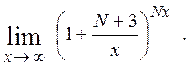
Завдання № 6. Обчислити похідні функцій:
1) ![]() , 2)
, 2) ![]() , 3)
, 3) 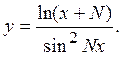
Завдання № 7.
1) Знайти частинні похідні даних функцій:
а) ![]() ; б)
; б) ![]() ;
;
в) 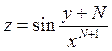 ; г)
; г) ![]()
2) Знайти градієнт даної
функції в точці А та похідну цієї функції в точці А за даним напрямом вектора ![]() :
:
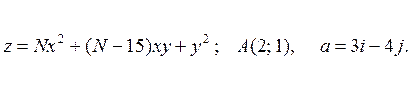
§3. ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ ДО ЗАВДАННЯ № 1
Література:[1], т. І, с. 99-117, [2], с. 129-152, [3], с. 31-64.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.