Навчально-методичний посібник для організації самостійної та індивідуальної роботи з дисципліни "Вища математика" (частина І), страница 29

, т. A (3;2), (3; -2)

Варіант 2. Знайти похідну:

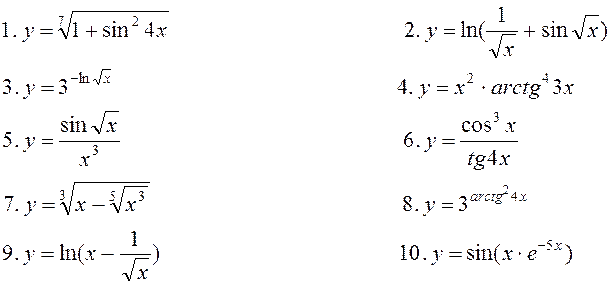
11. Знайти частинні похідні для функцій

;

.

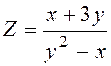12.Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (3;1), (1; -2)

Варіант 3. Знайти похідну:

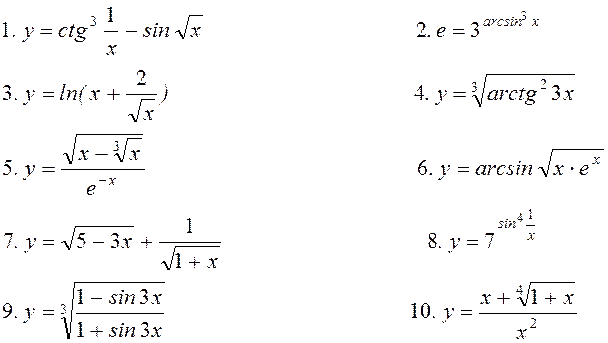
11. Знайти частинні похідні для функцій

;

.

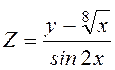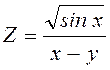12.Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (2;1), (1; -4)

Варіант 4. Знайти похідну:

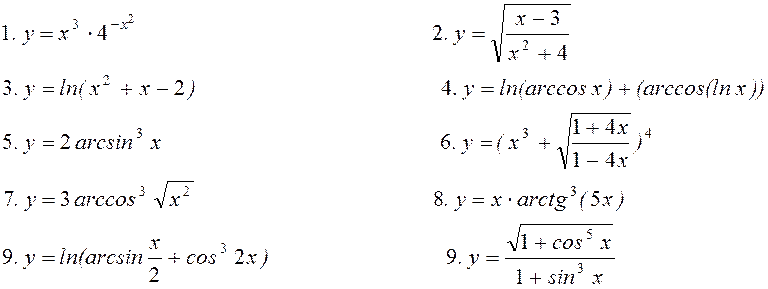11. 11.Знайти частинні похідні для функцій

;

.

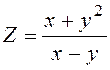12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (3;4), (2;1)

Варіант 5. Знайти похідну:

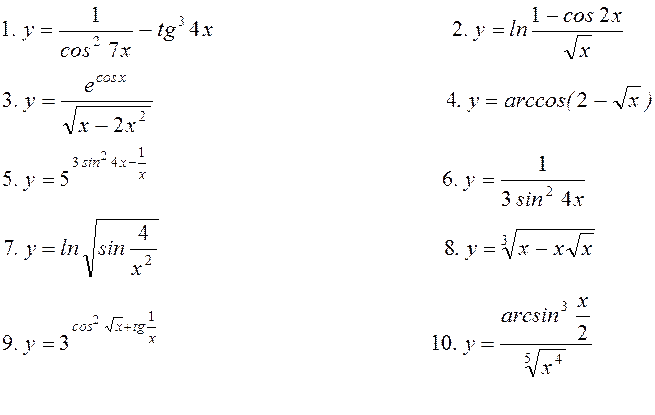
11. Знайти частинні похідні для функцій

;

.

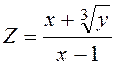12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (1;2), (4; -3)

Варіант 6. Знайти похідну:

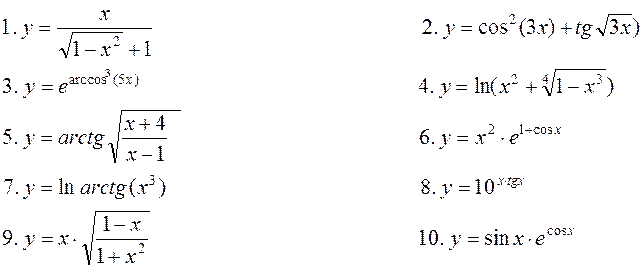
11. Знайти частинні похідні для функцій

;

.

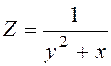12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (2;1), (4; -3)

Варіант 7. Знайти похідну:

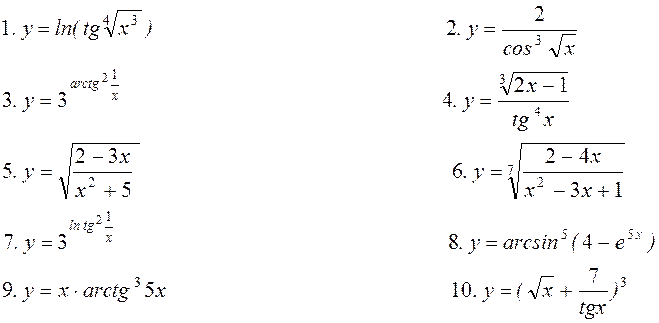
11. Знайти частинні похідні для функцій

;

.

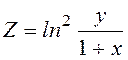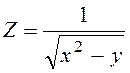12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (2;1), (2; -3)

Варіант 8. Знайти похідну:

11. Знайти частинні похідні для функцій

;

.

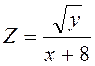12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (3;3), (3; -1)

Варіант 9. Знайти похідну:

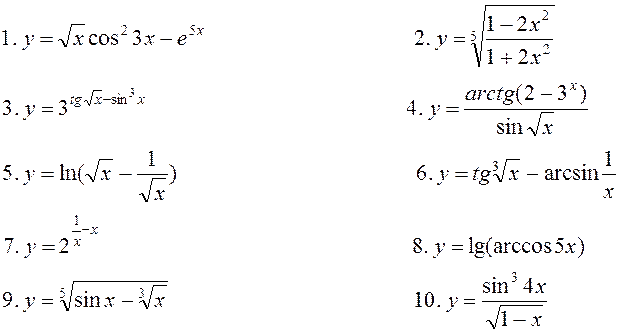
11. Знайти частинні похідні для функцій

;

.

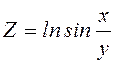12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (1;-1), (3; 1)

Варіант 10. Знайти похідну:

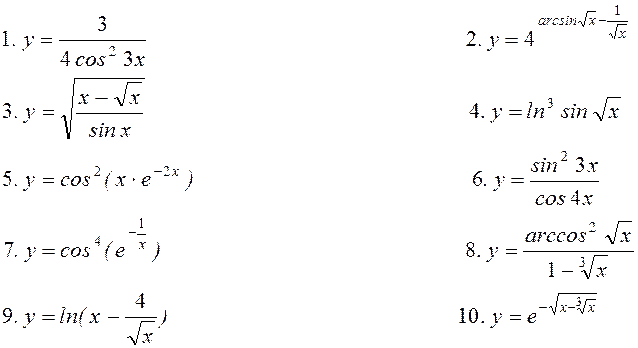
11. Знайти частинні похідні для функцій

;

.

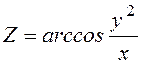12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (1;3), (1; -1)

Варіант 11. Знайти похідну:

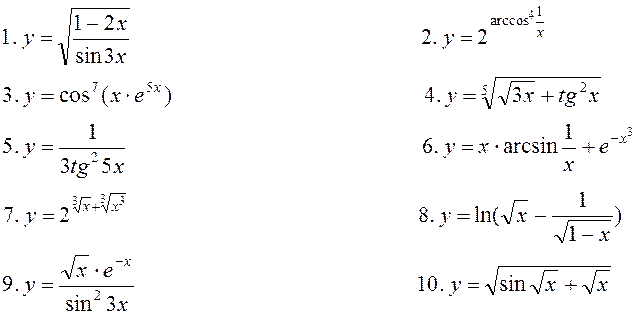
11. Знайти частинні похідні для функцій

18.;

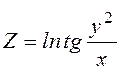19..

12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (2;-1), (3; 4)

Варіант 12. Знайти похідну:

 

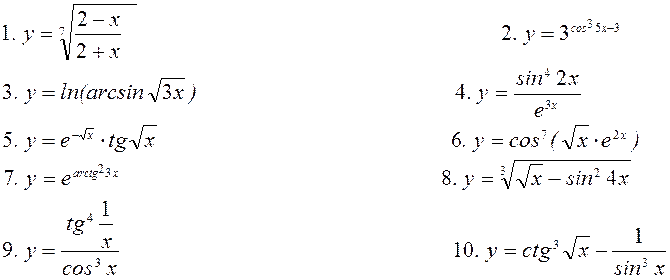
11. Знайти частинні похідні для функцій

;

.

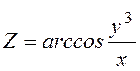12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (1;3), (-5; 12)

Варіант 13. Знайти похідну:

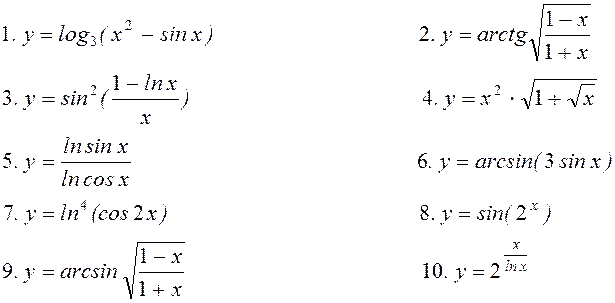
11. Знайти частинні похідні для функцій

;

.

12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (1;1), (2; -1)

аріант 14. Знайти похідну:

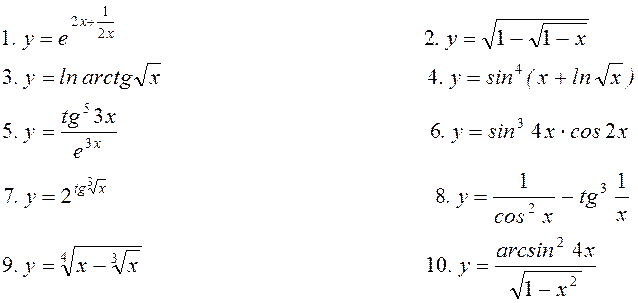
11. Знайти частинні похідні для функцій

;

.

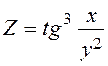12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (1;2), (5; -2)

Варіант 15. Знайти похідну:

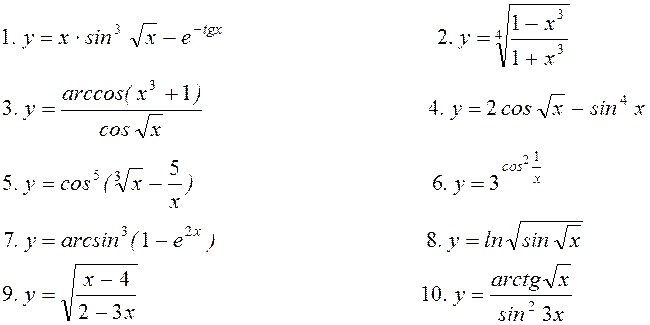
11. Знайти частинні похідні для функцій

;

.

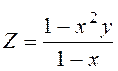12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (1;-2), (6; -8)

Варіант 16. Знайти похідну:

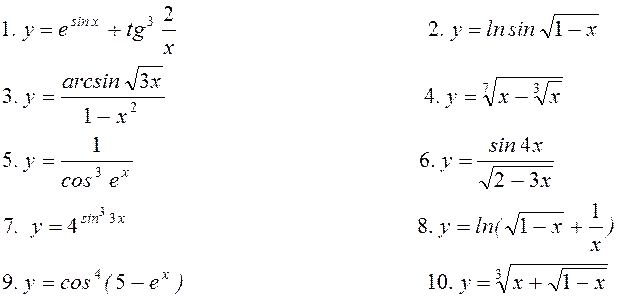
11. Знайти частинні похідні для функцій

;

.

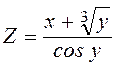12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (4;1), (2; 1)

Варіант 17. Знайти похідну:

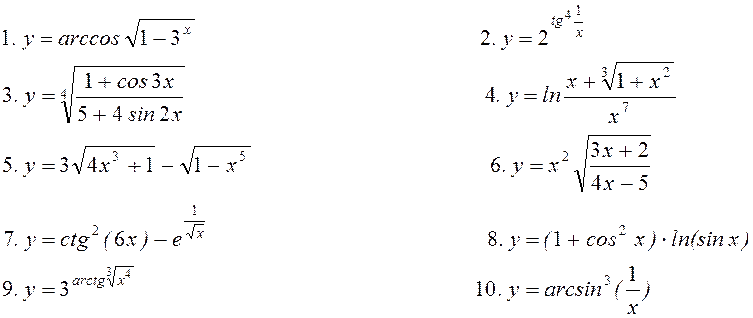
11. Знайти частинні похідні для функцій

;

.

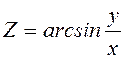12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (-1;3), (5; -1)

Варіант 18. Знайти похідну:

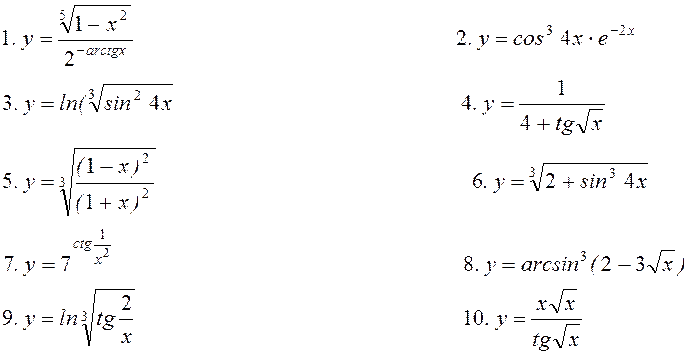
11. Знайти частинні похідні для функцій

;

.

12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (2;-1), (3; 4)

Варіант 19. Знайти похідну:

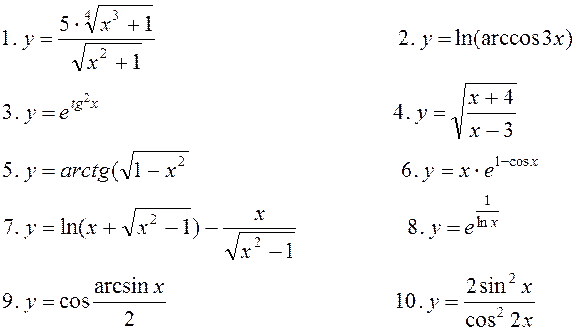
11. Знайти частинні похідні для функцій

;

.

12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (2;-1), (3; -4)

Варіант 20. Знайти похідну:

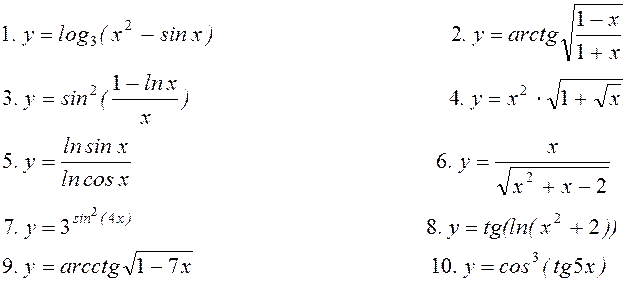
11. Знайти частинні похідні для функцій

;

.

12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (1;-1), (3; -4)

Варіант 21. Знайти похідну:

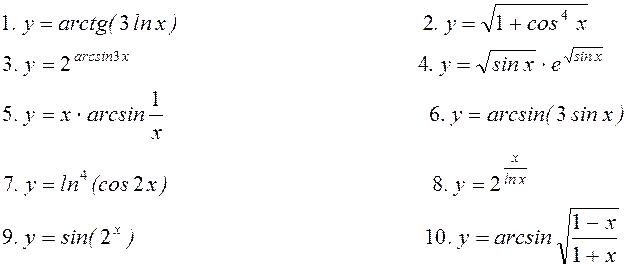
11. Знайти частинні похідні для функцій

;

.

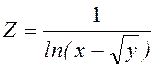12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (1;2), (4;3)

Варіант 22. Знайти похідну:

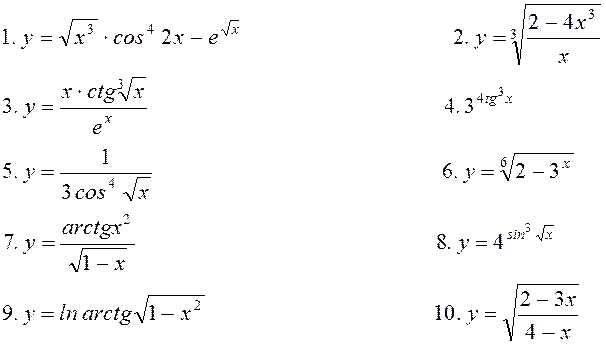
11. Знайти частинні похідні для функцій

;

.

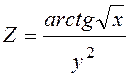12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (1;-2), (1; -3)

Варіант 23. Знайти похідну:

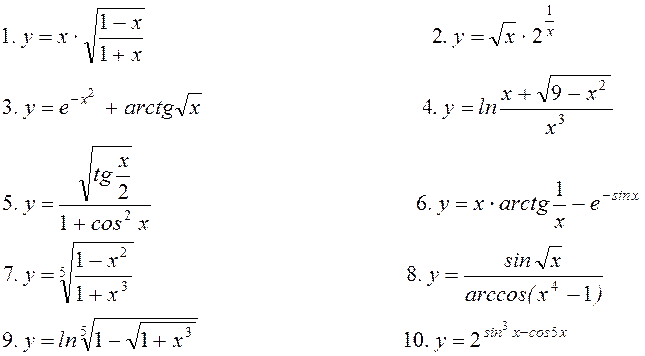
11. Знайти частинні похідні для функцій

;

.

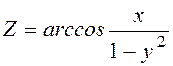12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (2;-2), (-3; 4)

Варіант 24. Знайти похідну:

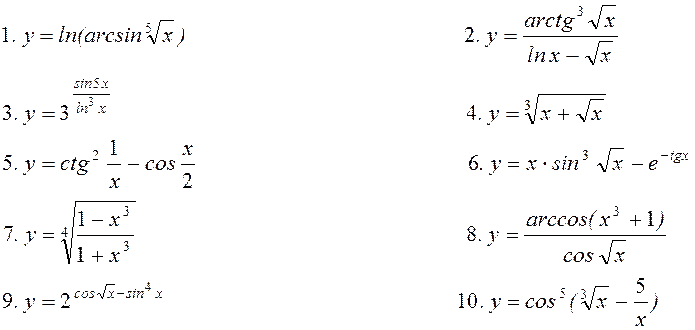
11. Знайти частинні похідні для функцій

;

.

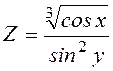12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (2;1), (1; 2)

Варіант 25. Знайти похідну:

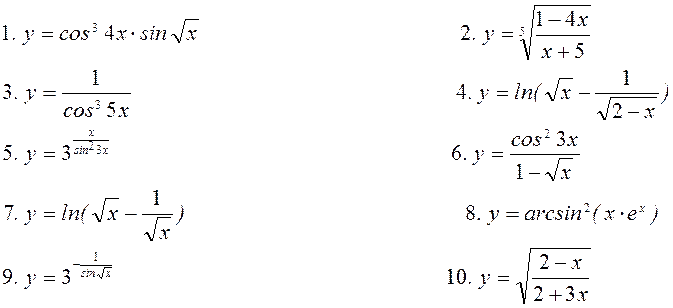
11. Знайти частинні похідні для функцій

;

.

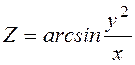12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (1;3), =

Варіант 26. Знайти похідну:

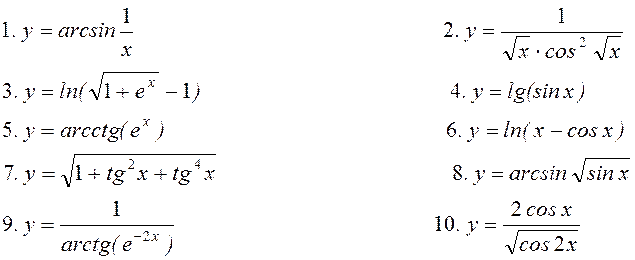
11. Знайти частинні похідні для функцій

;

.

12. Знайти градієнт функції в т. А та похідну за напрямом вектора

, т. A (2;1), (3; -4)