25. Маємо точки А(-1;
3; -7), В(2; -1; 5) та С(0; 1; -5). Обчислити: 
26. Маємо вершини чотирикутника А(1; -2; 2), В(1; 4; 0), С(-4; 1; 1) та D(-5; -5; 3). Довести, що його діагоналі АС та ВD взаємно перпендикулярні.
27. Визначити, при 
взаємно
перпендикулярні.
28. Маємо вершини трикутника А(-1; -2; 4), В( -4; -2; 0) та С(3; -2; 1). Визначити його внутрішній кут при вершині В.
29. Обчисливши внутрішні кути трикутника А(1; 2; 1), В(3; -1; 7), С(7; 4; -2), впевніться, що цей трикутник рівнобедрений.
30. Вектор 
, колінеарний вектору 
=(6; -8; -7,5), утворює гострий кут з віссю
Oz.
Знаючи, що |
|=50, знайти його координати.
31. Знайти вектор , який колінеарний вектору
=(2; 1; -1) і задовольняє умові 
32. Маємо два вектори: =(3; -1; 5)
та 
(1; 2; -3).
Знайти вектор при умові, що він
перпендикулярний до осі Oz і задовольняє умовам: 
33. Маємо пряму 2х+3у+4=0. Скласти рівняння прямої, що проходить через точку М0(2;1): 1) паралельно даній прямій; 2) перпендикулярно до даної прямої.
34. Маємо рівняння двох сторін трикутника 2х-3у+5=0, 3х+2у-7=0 і одна з його вершин А(2; -3). Скласти рівняння двох інших сторін цього прямокутника.
35. Знайти точку Q, симетричну точці P(-5; 13) відносно прямої 2х-3у-3=0.
36. Маємо середини сторін трикутника М1(2; 1), М2(5; 3) та М3(3; -4). Скласти рівняння його сторін.
37. Скласти рівняння прямої, якщо точка Р(2; 3) є основою перпендикуляра, опущеного з початку координат на цю пряму.
38. Сторони трикутника задані рівняннями 4х-у-7 =0, х+3у-31=0, х+5у-7=0. Визначити точку перетину його висот.
39. Маємо вершини трикутника А(1; -1), В(-2; 1) та С(3; 5). Скласти рівняння перпендикуляра, опущеного з вершини А на медіану, проведену з вершини В.
40. Знайти проекцію точки Р(-8; 12) на пряму, що проходить через точки А(2; -3) та В(-5; 1).
41. Визначити кут j між двома прямими:
1) 5х-у+7=0, 3х+2у=0; 2) 3х-2у+7=0, 2х+3у-3=0.
42. Точка А(-4; 5) є вершиною квадрата, діагональ якого лежить на прямій 7х-у+8=0. Скласти рівняння сторін і другої діагоналі цього квадрата.
43. Маємо дві протилежні вершини квадрата А(-1; 3) та С(6; 2). Скласти рівняння його сторін.
44. Встановити, які з вказаних пар прямих перпендикулярні:
1)3х-у+5=0, 2) 3х-4у+1=0, х+3у-1=0; 4х-3у+7=0.
45. Визначити кут j , утворений двома прямими:
1)3х –у +5 =0, 2х +у –7 =0;
46. Маємо дві вершини трикутника М1(-10; 2) та М2(6; 4); його висоти перетинаються в точці N(5; 2). Визначити координати третьої вершини М3.
47. Маємо дві вершини А(3; -1) та В(5; 7) трикутника АВС і точку N(4; -1) перетину його висот. Скласти рівняння сторін цього трикутника.
48. Знайти радіус і координати центра кола, заданого рівнянням х2+у2+8у-10х+37=0.
49. Встановити, яка лінія визначена рівнянням 4х2+9у2-8х+36у+4=0, і побудувати цю лінію.
50. Маємо дві точки М1(3; -1; 2) та М2(4; -2;
-1).Скласти рівняння площини, що проходить через точку М1
перпендикулярно вектору 
.
51. Скласти рівняння площини, що проходить через три точки:
М1(3; -1; 2), М2(4; -1; -1) та М3(2; 0; 2), знайти відстань від точки Р(-2; 1; 0) до цієї площини.
52. Визначити, при яких значеннях l та m вказані пари рівнянь будуть визначати паралельні площини:
1) 2x +Ly +3z -5=0, mx- 6y -6z + 2=0;
2) 3x –y +Lz -9=0, 2x+ my +2z –3 =0.
53. Визначити, при яких значеннях L вказані пари рівнянь будуть визначати перпендикулярні площини:
1) 3x -5y +Lz -3=0, x+ 3y +2z + 5=0;
2) 5x –y -3z -3=0, 2x+ Ly -3z + 1 =0;
3) 7x -2y -z =0, Lх+ y -z – 1=0.
54. Визначити двогранні кути, утворені перетином таких пар площин:
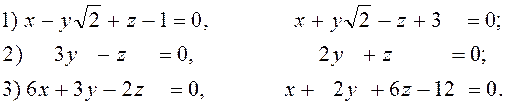
55. Скласти рівняння площини, що проходить через початок координат паралельно площині 5х –3у +2z –3 =0.
56. Скласти рівняння площини, що проходить:
1) через точку М1(3; -2; -7) паралельно площині 2х –3z +5 =0;
2) через О(0,0,0);
3) через М1|| XOY;
4) через М1 і вісь OZ.
57. Встановити, що три площини x -2y +z –7 =0, 2x +y –z +2 =0, x -3y +2z –11 =0 мають одну загальну точку, і обчислити її координати.
58. Обчислити відстань d від точки Р(-1; 1; -2) до площини, що проходить через точки М1(1; -1; 1), М2(-2; 1; 3) та М3(4; -5; -2).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.