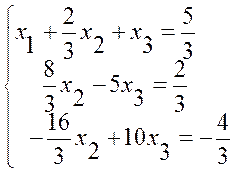
Ділимо друге рівняння на ![]() і виключаємо х2
з третього рівняння
і виключаємо х2
з третього рівняння
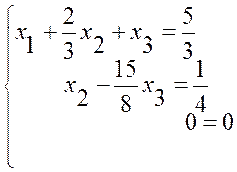
Останнє рівняння є тотожністю, його можна відкинути. Одержимо систему
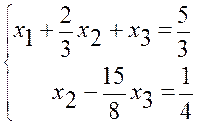
Покладаємо х3 = t. Тоді з другого рівняння
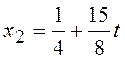
і з першого рівняння
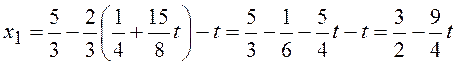 .
.
Таким чином, загальний розв’язок системи рівнянь має вигляд
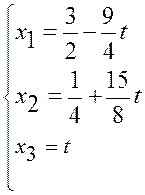 , де t може приймати будь-які числові значення.
, де t може приймати будь-які числові значення.
Відповідь: 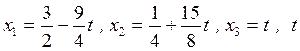 - будь-яке
число.
- будь-яке
число.
3.6. Розв’язати систему лінійних рівнянь, наведену у прикладі 1, методом Жордана – Гаусса.
|
х |
у |
z |
bi |
|
||
|
2 |
2 3 -1 |
-1 1 -1 |
-3 -1 3 |
-1 5 2 |
||
|
0 0 1 |
3 5 -1 |
0 3 -1 |
-6 -7 3 |
-3 1 2 |
||
|
0 0 1 |
5 -1 |
0 3 -1 |
-2 -7 3 |
-1 1 2 |
||
|
0 0 1 |
1 0 0 |
0 3 -1 |
-2 3 1 |
-1 6 1 |
||
|
0 1 |
1 0 0 |
0 -1 |
-2 1 1 |
-1 2 1 |
||
|
0 0 1 |
1 0 0 |
0 1 0 |
-2 1 2 |
-1 2 3 |
Пояснення до розрахункової таблиці
Обираємо розв’язувальний елемент а31 (розв’язувальний рядок – третій). Елементи стовпця контрольної суми ( S ) обчислюємо як суму елементів відповідного рядка (наприклад, для першого рядка: 1 + 2 + (-1) + (-3) = -1).
Шляхом елементарних перетворень (множенням елементів розв’язувального рядка на (-1) і додаванням до відповідних елементів першого рядка та множенням елементів розв’язувального рядка на (-2) і додаванням до відповідних елементів другого рядка) обчислимо всі елементи першого та другого рядків, у тому числі і елементи стовпця контрольної суми (розв’язувальний рядок залишається без змін). У результаті виконаних дій одержуємо одиничний вектор у розв’язувальному стовпці. Робимо перевірку правильності розрахунків, порівнюючи суму елементів кожного рядка з відповідним елементом контрольного стовпця.
На другому кроці розв’язувальним елементом може бути обраний будь-який, що не розташований у третьому рядку та першому стовпці, так як на першому кроці розв’язувальним був елемент а31. Обираємо, наприклад, а12 (тепер розв’язувальний рядок – перший). Слід звернути увагу на коефіцієнт при розв’язувальному елементі: він повинен дорівнювати одиниці. Щоб виконати дану умову, необхідно елементи розв’язувального рядка помножити на 1/3, і далі виконувати дії, як і на попередньому кроці. Таким чином, одержимо три одиничних вектори у перших трьох стовпцях розрахункової таблиці. Розв’язок системи знайдемо у стовпці вільних членів (bі) проти відповідних одиниць ( з першого рядка: у = -2, з другого рядка: z = 1, з третього рядка: х = 2).
Відповідь: x = 2, y = -2, z = 1.
3.7. Дослідити систему на сумісність.
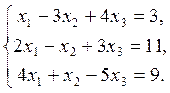
Виконаємо елементарні перетворення над розширеною матрицею системи:
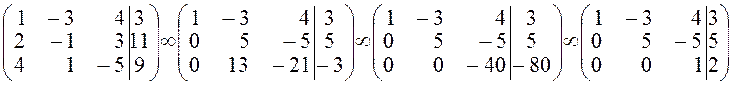 .
.
Визначимо ранг матриці А, розширеної матриці та кількість невідомих системи рівнянь:
r (A) = r (A*) = n = 3
За теоремою Кронекера-Капеллі система визначена і сумісна.
Задачі, рекомендовані до розв’язання на практичних заняттях з розділу 3
1. Розв`язати системи лінійних рівнянь за правилом Крамера, матричним методом, методом Гаусса та Жордана-Гаусса.
1) 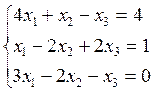 2)
2) 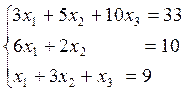
3) 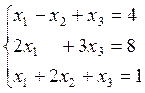 4)
4) 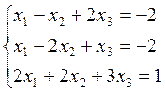
5) 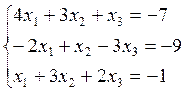 6)
6) 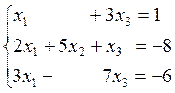
7) 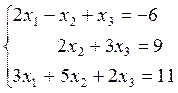 8)
8) 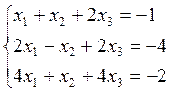
9) 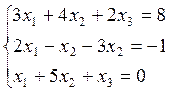 10)
10) 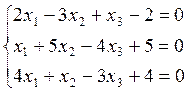
2. Розв’язати системи лінійних рівнянь методами Гаусса та Жордана- Гаусса:
|
1) х1 + х2 +2х3 +3х4 = 1 3х1 - х2 - х3 -2х4 = -4 2х1 + 3х2 - х3 - х4 = -6 х1 + 2х2 +3х3 - х4 = -4 |
2) х1 + 2х2 +3х3 -2х4 = 6 2х1 - х2 -2х3 -3х4 = 8 3х1 +2х2 -х3 +2х4 = 4 2х1 -3х2 +2х3 +х4 = -8 |
|
3) х1 + 2х2 +3х3 +4х4 = 5 2х1 + х2 +2х3 +3х4 = 1 3х1 + 2х2 + х3 +2х4 = 1 4х1 + 3х2 +2х3 + х4 = -5 |
4) х2 - 3х3 +4х4 = -5 х1 - 2х3 +3х4 = -4 3х1 + 2х2 -5х4 = 12 4х1 + 3х2 -5х3 = 5 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.