Навчально-методичний посібник для організації самостійної та індивідуальної роботи з дисципліни "Вища математика" (частина І), страница 14

Галузь	Споживання			Скінченний продукт	Валовий випуск	Скінченний продукт (новий)	Валовий випуск (новий)
	№1	№2	№3
№1	5	35	20	40	100	60	152,1
№2	10	10	20	60	100	70	135,8
№3	20	10	10	10	50	30	92,5

Розв’язання. Знайдемо спочатку матрицю А: елементи шуканої матриці А дорівнюють обсягу продукції і-ої галузі, що споживається на виробництво одиниці продукції j-ої галузі. Тому для знаходження елементів і-го стовпця матриці А треба поділити обсяг продукції і-ої галузі, вказаний у таблиці, на загальний валовий випуск цієї галузі. Таким чином, ми одержимо матрицю, що має вигляд:

;

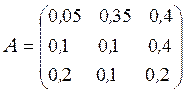X = (Е - А) · Y

Е – А = 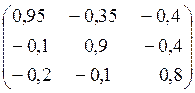;      det (E - A) = 0,514.

Матриця повних витрат:

(E – A) = .

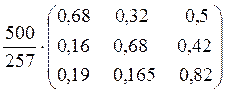Помноживши матрицю (Е - А) на вектор-стовпець Y кінцевих продуктів, дістанемо новий валовий випуск продукції:

Х = .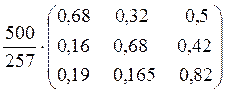

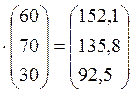Таким чином, першій галузі треба виробити 152,1 одиниць продукції, другій галузі – 135,8, третій галузі – 92,5.

4.4. Знайти власні значення і власні вектори матриці .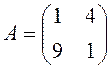

Розв’язання. Складаємо характеристичне рівняння

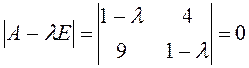 або , звідки власні значення матриці: .

Знаходимо власний вектор , відповідний власному значенню . Для цього розв’яжемо матричне рівняння

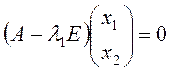 або 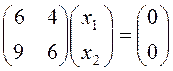, звідки знаходимо х₂= –1,5х₁. Поклавши х₁=с, одержимо, що вектори  при будь-якому с≠0 є власними векторами матриці з власним значенням  .

Аналогічно можна переконатися в тому, що вектори 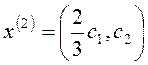при будь-якому с₁≠0 є власними векторами матриці з власним значенням .

4.5. Структурна матриця торгівлі чотирьох країн має вигляд:

А=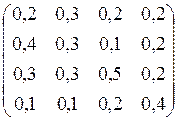

Знайти бюджети цих країн, що задовольняють збалансовану бездефіцитну торгівлю за умовою, що сума бюджетів:.

Розв’язання.

Власне значення матриці А  l=1 знаходимо з рівняння  det(A-lE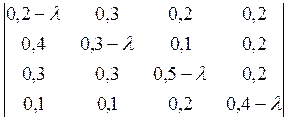)=0:

=0,

(A-E)C=0,

=,

.

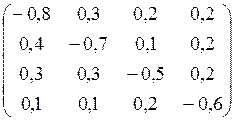
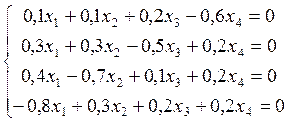Розв’яжемо отриману систему (наприклад, методом Гаусса):

             

  

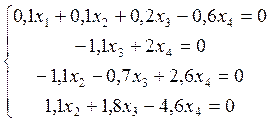
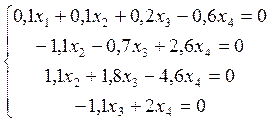
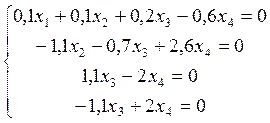
Система невизначена.

,

,

,

.

.

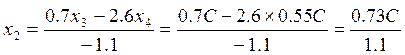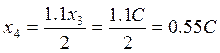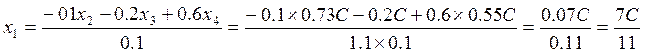Тоді     ,   ,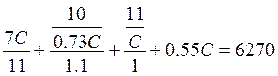

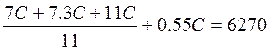2.3C+0.55C=6270,    2.85C=6270,         C=2200.

Отже, ,   ,    ,    .

4.6. Довести, що квадратична форма є додатно визначеною.

Розв’язання. Перший спосіб. Матриця А квадратичної форми має вигляд 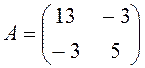. Для матриці А характеристичне рівняння:

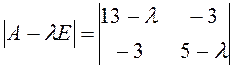  або  .

Розв’язуючи рівняння, знайдемо λ₁=14, λ₂=4. Оскільки корені характеристичного  рівняння матриці А додатні, то квадратична форма  L- додатно визначена.

Другий спосіб. Оскільки головні мінори матриці

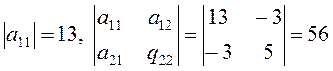
додатні, то за критерієм Сильвестра дана квадратична форма L додатно визначена.

4.7. З однієї фірми на іншу необхідно перевезти обладнання трьох типів: 1 типа - 95 од., 2 тип -100 од. , 3 тип - 85 од. Для перевезення обладнання фірма може замовити транспорт трьох видів . Кількість обладнання, що розміщується на визначеному виді транспорту, приведено в такій таблиці:

Тип	Вид транспорту
обладнання	T1	T2	T3
I	3	2	1
II	4	1	2
III	3	5	4

Записати в математичній формі умову перевезення обладнання з однієї фірми на іншу і визначити, скільки одиниць транспорту кожного виду використовується під час перевезення.

Розв’язання:

Умови перевезення обладнання визначаються системою рівнянь:

Знайдемо кількість транспорту кожного виду:

Відповідь:під час перевезення обладнання з однієї фірми на іншу використовується 15 одиниць транспорту першого виду, 20 одиниць транспорту другого виду і 10 одиниць транспорту третього виду.

4.8. Підприємство випускає продукцію трьох видів А, В, С. Рівень випуску визначається обмеженістю ресурсів. Всі числові дані приведені в такій таблиці:

Ресурси	Запаси	Норми витрат на одиницю часу
	ресурсу	А	В	С
Сировина, (кг)	24	5	7	4
Обладнання, (од.)	10	5	2	1
Матеріали, (кг)	75	10	5	20