3. Розв’язати системи лінійних рівнянь методом Гаусса
1) 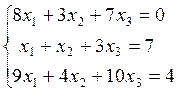 2)
2)
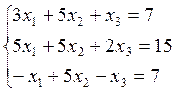
3) 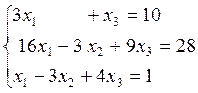 4)
4)
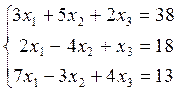
5) 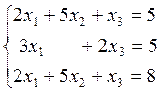 6)
6)
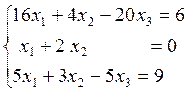
7) 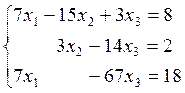 8)
8) 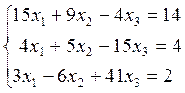
9) 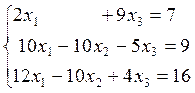 10)
10)
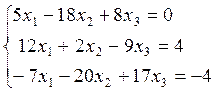
4. Дослідити дані системи на сумісність:
|
1) |
2) |
|
3) |
4) |
|
5) |
6) |
|
7) 2х1 - х2 +3х3 +2х4 = 4 3х1 +3х2 +3х3 +2х4 = 6 3х1 - х2 - х3 +2х4 = 6 3х1 - х2 +3х3 - х4 = 6 |
8) х1 + 3х2 +5х3 +7х4 = 12 3х1 + 5х2 +7х3 + х4 = 0 5х1 + 7х2 + х3 +3х4 = 4 7х1 + х2 +3х3 +5х4 = 16 |
|
9) 2х1 - х2 + х3 - х4 = 1 2х1 - х2 -3х4 = 2 3х1 - х3 + х4 = -3 2х1 + 2х2 -2х3 +5х4 = -6 |
10) х1 + 2х2 +3х3 +4х4 = 11 2х1 + 3х2 +4х3 + х4 = 12 3х1 + 4х2 + х3 +2х4 = 13 4х1 + х2 +2х3 +3х4 = 14 |
Розділ 4. ЕЛЕМЕНТИ МАТРИЧНОГО АНАЛІЗУ
Основні питання, що виносяться на практичні заняття за розділом 4:
1. Аналіз обсягів випуску продукції.
2. Розв’язання задач на складання міжгалузевого балансу.
3. Міжнародна модель торгівлі
4. Встановлення характеру знаковизначеності квадратичної форми.
Після опрацювання розділу на практичних заняттях студент повинен
знати: основні методи і моделі матричного аналізу в дослідженні економічних проблем.
вміти: застосовувати матриці і системи рівнянь в економічному аналізі.
Рекомендована література:
[1], т. І, с. 121-123.
[2], с. 153-180,192-197.
[3], с. 65-81.
Рекомендації до розв’язання типових прикладів розділу 4
4.1. Підприємство виробляє три види продукції П1, П2, П3, використовуючи два види сировини S1, S2. Норми витрат сировини задані таблицею:
|
П1 |
П2 |
П3 |
|
|
S1 |
5 |
0 |
4 |
|
S2 |
3 |
1 |
4 |
Визначити витрати сировини, необхідні для вироблення П1 =150 од., П2 =120 од., П3 =80 од.
Розв’язання. Представимо норми витрат у вигляді матриці 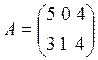 , а обсяг потрібної для вироблення
продукції – у вигляді вектора-стовпця
, а обсяг потрібної для вироблення
продукції – у вигляді вектора-стовпця 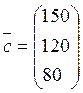 . Якщо
розглядати шуканий обсяг витрат сировини у вигляді вектора-стовпця
. Якщо
розглядати шуканий обсяг витрат сировини у вигляді вектора-стовпця 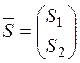 , то його можна знайти як добуток
, то його можна знайти як добуток ![]()
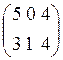
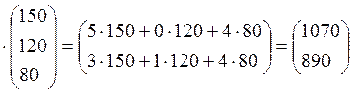 .
.
Таким чином, для вироблення вказаного обсягу продукції необхідно витратити 1070 од. сировини S1 та 890 од. сировини S2.
4.2. З деякого листового матеріалу треба викроїти 200 заготовок типу А, 260 – типу В і 290 – типу С. При цьому можна використовувати три типи розкрою. Кількість заготовок, отриманих з кожного листа при кожному способі розкрою, вказана у таблиці:
|
Тип заготовки |
Спосіб розкрою |
||
|
1 |
2 |
3 |
|
|
А |
3 |
2 |
1 |
|
В |
1 |
6 |
2 |
|
С |
4 |
1 |
5 |
Встановити, скільки необхідно мати листів для того, щоб викроїти вказану кількість заготовок.
Розв’язання. Позначимо через х1, х2, х3 кількість листів матеріалу, які розкроюють відповідно до перших, других та третіх способів. Тоді при першому способі розкрою х1 листів буде одержано 3х1 заготівок типу А, при другому - 2х2, при третьому - 1х3. Для повного виконання завдання по заготівкам типу А сума 3х1+2х2+х3 має дорівнювати 200, тобто 3х1+2х2+х3=200.
Аналогічно одержимо рівняння
х1+6х2+2х3=260,
4х1+х2+5х3=290, яким повинні задовольняти невідомі х1, х2, х3 для того, щоб виконати завдання по заготівках В і С.
Система лінійних рівнянь
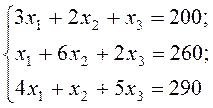
виражає в математичній формі умови виконання всього завдання по заготівках А, В, С.
Розв’язавши одержану систему одним з відомих методів, отримаємо, що для розкрою вказаної кількості заготовок необхідно мати x1=40, x2=30, x3=20 листів матеріалу для розкрою відповідно першим, другим і третім способами.
4.3. Знайти необхідний валовий випуск продукції, коли кінцевий продукт буде інший. Дані подамо таблицею:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.