Рекомендована література:
[1], т. І, с.174-180, с.180-194
[2], с.337-360
[3], с. 177-185, с.186-214
Рекомендації до розв’язання типових прикладів розділу 6
6.1. Знайти 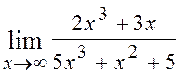 .
.
Розв¢язання. Маємо невизначеність ![]() . В
подібних випадках чисельник і знаменник треба розділити на найвищий степінь х,
що входить до них
. В
подібних випадках чисельник і знаменник треба розділити на найвищий степінь х,
що входить до них
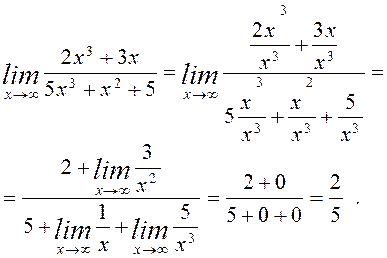
6.2. Знайти 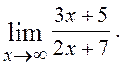
Розв¢язання. Чисельник і знаменник дробу необмежено зростають при ![]() В такому випадку кажуть, що має місце
невизначеність виду
В такому випадку кажуть, що має місце
невизначеність виду ![]() . Розділивши на х чисельник і
знаменник дробу, одержимо:
. Розділивши на х чисельник і
знаменник дробу, одержимо:
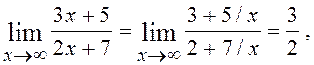
тому що при х → ¥ кожен з дробів 5/х і 7/х прямують до нуля.
6.3. Знайти 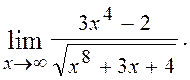
Розв¢язання. Розділимо чисельник і знаменник на х4:
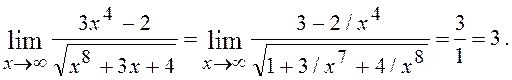
6.4. Знайти 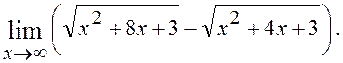
Розв¢язання. Має місце невизначеність виду ¥ - ¥. Помножимо і розділимо вираз на спряжений
![]()
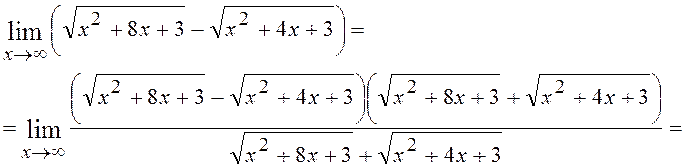
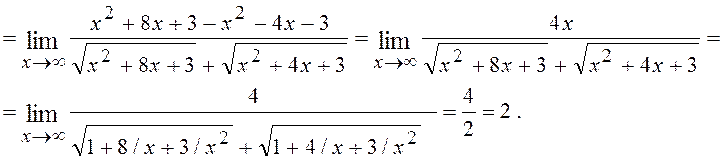
6.5. Знайти 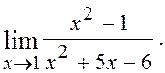
Розв¢язання. Підстановка значення х=1 під знак границі приводить
до невизначеності ![]() Розкладемо чисельник і знаменник
на множники і скоротимо на х-1 (х ≠ 1):
Розкладемо чисельник і знаменник
на множники і скоротимо на х-1 (х ≠ 1):
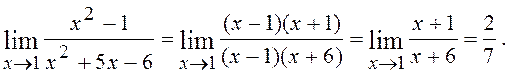
6.6. Знайти 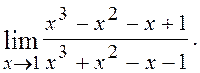
Розв¢язання. Має місце невизначеність виду 0/0. Розкладемо на множники чисельник і знаменник дробу:
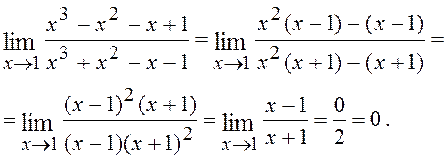
6.7. Знайти 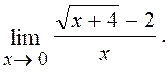
Розв¢язання. Помножимо чисельник і знаменник дробу на суму ![]()
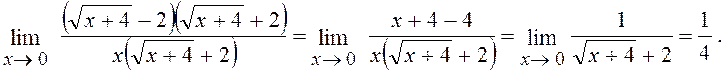
6.8. Знайти 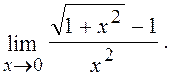
Розв¢язання. Маємо невизначеність виду ![]() щоб її
розкрити, множимо чисельник і знаменник на вираз, спряжений чисельнику. Після
цього можна скоротити на х2 і скористатися теоремою про границю
дробу
щоб її
розкрити, множимо чисельник і знаменник на вираз, спряжений чисельнику. Після
цього можна скоротити на х2 і скористатися теоремою про границю
дробу
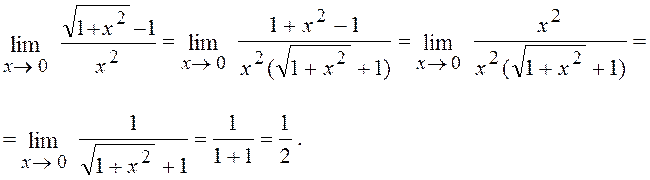
6.9. Знайти 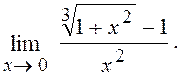
Розв¢язання. Множимо чисельник на такий множник, щоб одержати різницю кубів, тобто
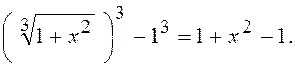
Згадаємо, що a3-b3=(a-b)(a2+ab+b2).
Прийнявши різницю ![]() за різницю основ, помічаємо, що її треба
домножити на неповний квадрат суми, тобто на
за різницю основ, помічаємо, що її треба
домножити на неповний квадрат суми, тобто на
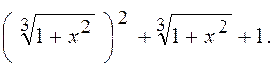
На цей множник треба помножити і знаменник:
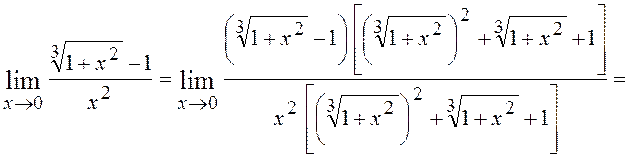
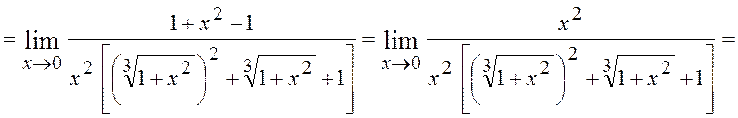
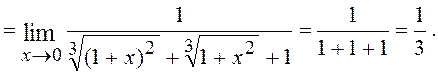
6.10. Знайти 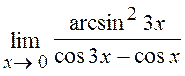 .
.
Розв¢язання. Згідно відомій тригонометричній формулі,
![]() cos 3x-cos x= -2sin 2x sinx.
cos 3x-cos x= -2sin 2x sinx.
Оскільки sinx ~ x, sin2x ~ 2x, arcsin23x ~(3x)2, (див. (1),(3))
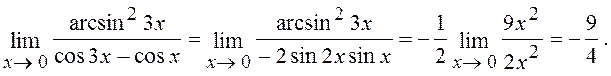
6.11. Знайти 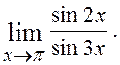
Розв¢язання. Чисельник і знаменник- нескінченно малі функції. Однак х не є нескінченно малою функцією (прямує не до нуля, а до p), тому співвідношення sin2x ~ 2x не має змісту. Введемо нескінченно малу a= p -х, тоді х= p -a і
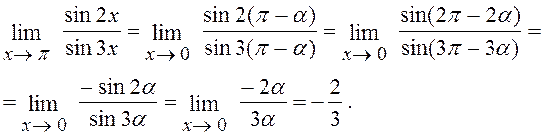
6.12. Знайти 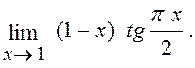
Розв¢язання. Зробимо попередню заміну змінної. Якщо ввести позначення х-1 = a, то a® 0 при х® 1; тоді,користуючись (2), маємо:
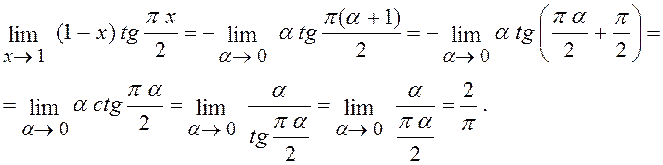
6.13. Знайти 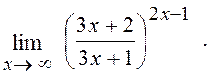
Розв¢язання. Маємо невизначеність 1¥, тоді за другою особливою границею (див.(6)):
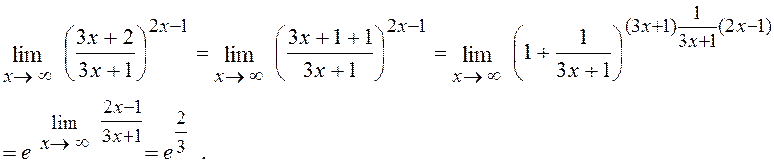
![]()
6.14. Знайти 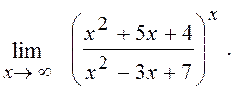
Розв¢язання. Діленням чисельника дробу на знаменник виділимо цілу частину:
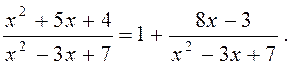
Таким чином, при х® ¥ ця функція представляє собою степінь, основа якого прямує до одиниці, а показник - до нескінченності (невизначеність виду 1¥). Перетворюючи функцію так, щоб використати другу особливу границю, одержимо
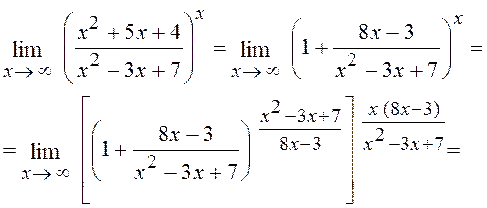
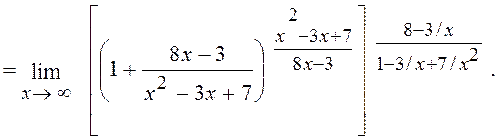
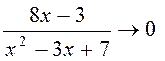
![]() при х® ¥, тому
при х® ¥, тому
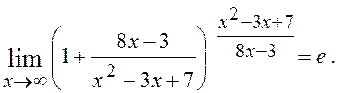
Прийнявши до уваги, що
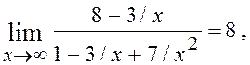 одержуємо
одержуємо
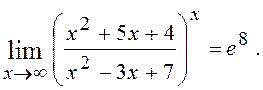 |
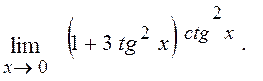
Розв¢язання. 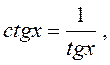 тому, користуючись (2)
та (7), маємо:
тому, користуючись (2)
та (7), маємо:
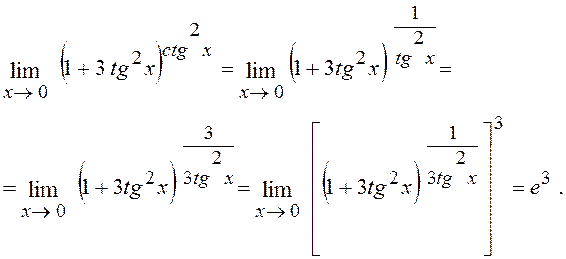
6.16. Знайти 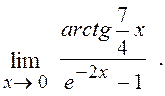
Розв¢язання. Оскільки 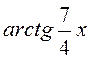 ~
~![]() при х® 0, (див.(4)), а
при х® 0, (див.(4)), а
e-2x-1 ~(-2x) при х®0 (див.(10)), то
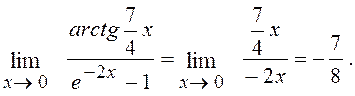
6.17. Знайти 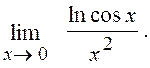
Розв¢язання.
lncosx = ln (1+cosx-1)~ cosx-1 (за формулою (8))
(a = cosx -1 ® 0 при х® 0).
За другим правилом граничного переходу, використовуючи (5), одержимо:
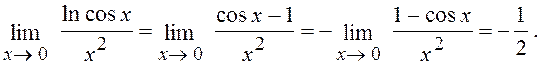
6.18.Дослідити на неперервність і знайти точки
розриву функції 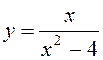 .
.
Розв’язання. Ця функція є дробово-раціональною, і тому вона неперервна в усіх точках, в яких знаменник відмінний від нуля. В точках х=±2 функція не визначена, і тому розривна. Неважко перевірити, що в обох цих точках односторонні границі нескінченні:
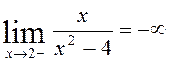 ,
, 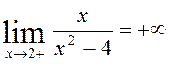 ,
, 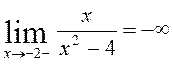 ,
, 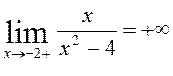 .
.
Отже, х=±2 – точки розриву другого роду.
6.19. Внесок А = 100.000 гр.од. вкладений під складні відсотки (6 %) терміном на три роки. Обчислити кінцеву суму, якщо відсотки нараховуються неперервно.
Розв’язання:Сума внеску обчислюється
за формулою 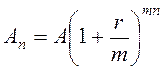 .
.
Але в
нашому випадку відсотки нараховуються неперервно при![]() , тоді формула
приймає вигляд:
, тоді формула
приймає вигляд:
An = 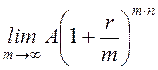 = Aern
= Aern
P = 100000·e0. 18 = 119.721 (гр.од.).
Задачі, рекомендовані до розв’язання на практичних заняттях з розділу 6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() 2.
Обчислити границі функцій
2.
Обчислити границі функцій
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.