3. Обчислити границі функцій
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Обчислити границі функцій
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Обчислити границі функцій
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Розв’язати задачі на економічний зміст числа е.
1) 2000 грн. внесено до банку за схемою неперервних відсотків за ставкою 10 %. Знайти нарощену суму через 1, 2, 3, 5 років.
2) За однаковою процентною ставкою за схемою неперервного нарахування відсотків пан Іванов через 2 роки отримує 1000 грн., а пан Іваненко через 4 роки отримує 600 грн. Знайти процентну ставку, якщо початковий внесок Іванова вдвічі більший, ніж Іваненка.
3) Знайти початковий борг, якщо боржник повинен заплатити кредитору 1000 грн. через 2 роки, 2500 грн. через 3 роки, 3000 грн. через 3,5 роки. Процентна ставка 6 % річних, нарахування неперервне.
7. Дослідити на неперервність функції:
1) 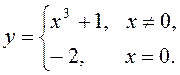 2)
2) 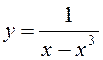 .
.
Розділ 7.ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ТА КІЛЬКОХ ЗМІННИХ
Основні питання, що виносяться на практичні заняття за розділом 7:
7. Обчислення похідної за допомогою таблиці похідних та основних правил диференціювання.
8. Обчислення похідної складної функції.
9. Похідні вищих порядків.
10.Обчислення похідних неявних функцій.
11.Знаходження рівняння дотичної до кривої.
12.Обчислення границь функцій за допомогою правила Лопіталя.
13.Обчислення частинних похідних першого та другого порядків.
14.Обчислення повного диференціалу функції двох змінних.
15.Знаходження градієнта функції.
16.Обчислення похідної за напрямом.
Після опрацювання розділу на практичних заняттях студент повинен
знати: поняття похідної функції однієї змінної та її геометричний, фізичний і економічний зміст, поняття диференціалу функції, таблицю похідних, основні правила диференціювання, формулу Тейлора, правило Лопіталя; поняття частинних похідних функції багатьох змінних, поняття повного диференціалу функції багатьох змінних, поняття похідної за напрямом та градієнту функції багатьох змінних;
вміти: обчислювати похідні функції однієї змінної за допомогою таблиці похідних та основних правил диференціювання, обчислювати похідні складної функції, похідні вищих порядків, похідні неявних функцій, знаходити рівняння дотичної до кривої, обчислювати границі функцій за допомогою правила Лопіталя; обчислювати частинні похідні функцій багатьох змінних першого та другого порядків, знаходити повний диференціал функції багатьох змінних, знаходити градієнт функції та похідну за напрямом.
Рекомендована література:
[1], т. І, с.200-217, 239-260.
[2], с.373-431.
[3], с. 217-262, 341-377.
Рекомендації до розв’язання типових прикладів розділу 7
7.1.![]()
Розв’язання.
Перепишемо задану функцію у вигляді y = x3/2×(3lnx-2).
Тоді
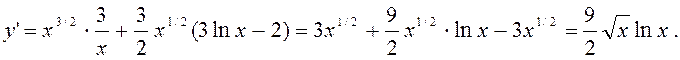
7.2. 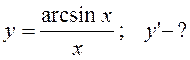
Розв’язання.
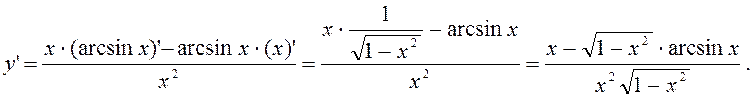
7.3. y=(sinx+4)3; y¢-?
Розв’язання. Маємо ступеневу функцію з показником 3 і основою sinx+4. Для знаходження похідної треба скористуватися спочатку правилом знаходження похідної складної степеневої функції,потім суми двох функцій sinx+4- синуса і константи:
y’=3(sinx+4)2(sinx+4)’=3(sinx+4)2×cosx .
y= ![]() ; y¢-?
; y¢-?
Розв’язання.
Маємо показову функцію з основою e і показником arctg3x ; функція arctg3x- степенева з показником 3 і основою arctgx.
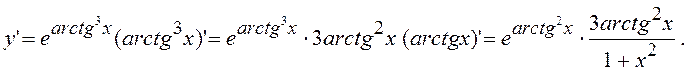
7.5. y=tg6x ; y¢-?
Розв’язання.
y¢=6tg5x×(tgx)’=6tg5x×sec2x .
7.6. y=cos2x; y¢-?
Розв’язання.
y¢=2cosx(cosx)¢=-2cosx×sinx=-sin2x .
7.7. y=sin(2x+3); y¢-?
Розв’язання.
y¢=cos(2x+3)×(2x+3)’=2cos(2x+3).
7.8. y=tg lnx ; y’-?
Розв’язання.
y’=sec2(lnx)
×(lnx)’=![]() × sec2lnx.
× sec2lnx.
7.9. 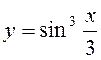 ; y’-?
; y’-?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.