Математика \ Высшая математика

Навчально-методичний посібник для організації самостійної та індивідуальної роботи з дисципліни "Вища математика" (частина І), страница 34

де аi– деякі числа (координати вектора).

Перед виконанням завдання № 2 рекомендується опрацювати приклади 5.1-5.6 глави ІІ.

§5. ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ ДО ЗАВДАННЯ № 3

Література: [1], т. І, с. 142-157, [2], с.239-250, [3], с. 116-167.

Основні види рівнянь прямої на площині:

Ax+By+C=0 – загальне рівняння прямої;

y=kx+b– рівняння прямої з кутовим коефіцієнтом; k=tgα, де α – кут між прямою і додатним напрямком осі Ох;

y-y0=k(x-x0) – рівняння прямої, яка проходить через дану точку (x0, y0) у даному напрямку;

A(x-x0)+B(y-y0)=0 – рівняння прямої, яка проходить через точку М(x0,y0) перпендикулярно до вектора  (до нормального вектора);

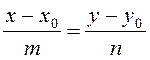 – рівняння прямої, яка проходить через точку М0(x0,y0) паралельно напрямному вектору  (канонічне рівняння);

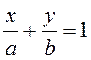 – рівняння прямої у відрізках (aі b– величини напрямлених відрізків, відрізуваних прямою на координатних осях);

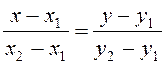 – рівняння прямої, яка проходить через дві дані точки М1(x1,y1) і М2(x2,y2).

Якщо задане загальне рівняння прямої, то її кутовий коефіцієнт визначається за формулою .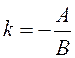

Якщо k1, k2– кутові коефіцієнти  двох прямих, то кут Θ між ними визначається за формулою .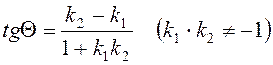

Умова паралельності двох прямих: k1=k2.

Умова перпендикулярності двох прямих: .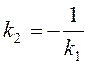

Якщо задані рівняння прямої Ax+By+C=0 і точка M0(x0,y0), то відстань від цієї точки до даної прямої обчислюється за формулою

.

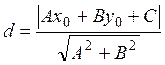Лінії другого порядку.

Нехай задане загальне рівняння другого ступеня з змінними xі y, яке не містить добутка  змінних: Ax2+By2+Cx+Dy+E=0.

Якщо цьому рівнянню відповідає лінія на площині, то це або еліпс, або гіпербола, або парабола. Для побудови кривої за допомогою її рівняння необхідно вилучити повні квадрати відносно кожної з змінних xіy, які містяться в рівнянні другого ступеня.

Якщо при цьому початкове рівняння перетворюється до виду 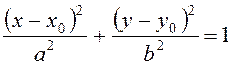, то це еліпс з центром у точці 01(x0,y0), напівосями aі b, а осі симетрії паралельні осям Ох і Oy.

Якщо при цьому початкове рівняння перетворюється до виду 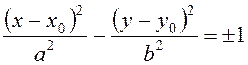, то це гіпербола з центром у точці 01(x0,y0) і характеристичним прямокутником з сторонами 2aі 2b. Діагоналі цього прямокутника є асимптотами гіперболи.

Якщо початкове рівняння перетворюється до виду , чи , то це парабола типу  чи  з вершинами в точці 01(x0,y0) і симетричні відносно прямих відповідно x= x0  іy= y0.

Перед виконанням завдання № 3 рекомендується опрацювати приклади 5.7-5.17 глави ІІ.

§6. ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ ДО ЗАВДАННЯ №4

Література: [1], т. І, с.162-169, [2], с.269-291, [3], с. 154-170.

Основні види рівнянь площини:

Ax+By+Cz+D=0 – загальне рівняння площини,  – вектор, нормальний (перпендикулярний) до цієї площини;

 – рівняння площини у відрізках, де a, b, с – довжини напрямлених відрізків, відрізуваних площиною на координатних осях;

A(x-x0)+B(y-y0)+C(z-z0)=0 – рівняння площини, яка проходить через задану точку  M0(x0,y0, z0,) перпендикулярно до нормального вектора :

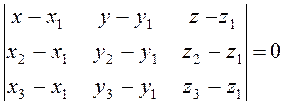– рівняння площини, яка проходить через три задані точки М1(x1,y1, z1) і М2(x2,y2, z2), М3(x3,y3, z3).

Умова паралельності двох площин A1x+B1y+C1z+D1=0 і A2x+B2y+C2z+D2=0 має вигляд 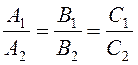, а умовою перпендикулярності цих же площин є рівність

A1A2+ B1B2+ C1C2=0.

Кут між двома даними площинами визначається за формулою

.

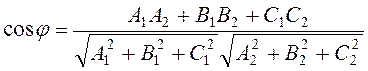Відстань  від точки M0(x0,y0, z0,) до площини   Ax+By+Cz+D=0:

.

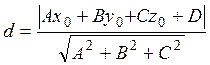При розв’язанні задач на пряму лінію у просторі використовуються такі рівняння:

1) 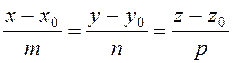 – каноничні рівняння прямої, де (x0,y0, z0,) –задана точка , а вектор – напрямлений вектор прямої;

2) 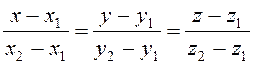– рівняння прямої, яка проходить через дві задані точки М1(x1,y1, z1) і М2(x2,y2, z2);

3)

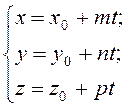
параметричні рівняння прямої у просторі, де  – деякий параметр;

4)

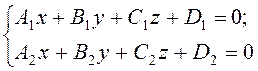
– загальні рівняння прямої, коли пряма лінія визначена перетином двох площин.

Кут між прямими 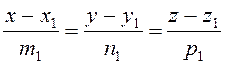 і  обчислюється за формулою

.

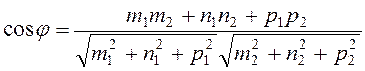Умова паралельності і перпендикулярності цих прямих відповідно:

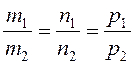  і .

Щоб знайти точку перетину прямої 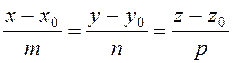 і площини Ax+By+Cz+D=0, слід розв’язати сумісно ці три рівняння.

Перед виконанням завдання № 4 рекомендується опрацювати приклади 5.18-5.29 глави ІІ.

§7. ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ ДО ЗАВДАННЯ №5

Література: [1], т. І, с.174-180, [3], с. 177-185.

Скачать файл