1. Частинний і повний прирости функції двох змінних та їх економічне тлумачення.
2. Частинні похідні функції двох змінних та їх геометричне тлумачення.
3. Частинні еластичності.
4. Повний диференціал функції двох змінних, його геометричний зміст та застосування до наближених обчислень.
5. Похідна за напрямом та градієнт функції двох змінних.
6. Частинні похідні та диференціали вищих порядків функції двох змінних.
Література:
[1], т. І, с.200-217, 239-260.
[2], с.373-431.
[3], с. 217-262, 341-377.
Задачі, рекомендовані до розв’язання:
[3], с.246, № 6.10-6.36; с. 280, № 7.8-7.23.
Питання для самоконтролю
1. Дайте визначення похідної. Її механічний і геометричний сенс.
2. Виведіть формули похідних суми, добутку і частки двох функцій. Приведіть приклади.
3. Виведіть формули диференціювання тригонометричних функцій.
4. Виведіть формули диференціювання степеневої, показникової і складної показникової функцій.
5. Сформулюйте визначення диференціала функції.
6. Для яких функцій диференціал тотожно рівний приросту?
7. Механічний, геометричний і економічний сенс другої похідної.
8. Як знаходять похідну функції, задану неявно?
9. Перерахуйте різні типи невизначеності, для розкриття яких можна використовувати правило Лопіталя. Приведіть приклади
10.Поняття функції двох і більшого числа змінних та їх інтерпретація в економічній теорії.
11.Область визначення та область значень функції, графічне зображення функцій.
12.Лінії рівня функції двох змінних та їх економічне тлумачення.
13.Поняття функції комплексної змінної. Виробничі функції багатьох змінних.
14.Заповнити
пусте місце будь-яким з можливих способів: 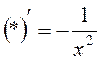 .
.
15.Заповнити
пусте місце будь-яким з можливих способів: 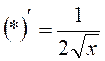 .
.
16.Заповнити
пусте місце будь-яким з можливих способів: 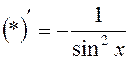 .
.
17.Заповнити
пусте місце будь-яким з можливих способів: 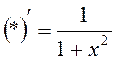 .
.
18.Заповнити
пусте місце будь-яким з можливих способів: 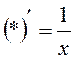 .
.
19.Частинні похідні функції двох змінних та їх економічне тлумачення.
20.Повний диференціал функції двох змінних, його геометричний зміст та застосування до наближених обчислень.
21. Похідна за напрямом та градієнт функції двох змінних.
22.Частинні похідні та диференціали вищих порядків функції двох змінних.
23.Як визначаються частинні похідні? Сформулювати правила знаходження частинних похідних функцій декількох змінних.
24.Який геометричний сенс частинних похідних функції z=f(x,y)?
25.Що називається повним приростом і повним диференціалом функції z=f(x,y)? Як виражається повний диференціал функції через її частинні похідні?
Результат виконання роботи: конспект, виконання домашнього завдання.
Форма контролю: перевірка конспекту,усне опитування, обговорення питань, тестування, контрольна робота за модулем № 3, складання, аналіз та обговорення практико-орієнтованих задач.
Розділ 8. ГРАНИЧНИЙ (МАРГІНАЛЬНИЙ) АНАЛІЗ
Тема 1.19. Застосування диференціального числення функції однієї змінної в економічному аналізі.
1. Граничні витрати, дохід і прибуток.
2. Максимізація прибутку і маргінальний аналіз.
3. Аналіз витрат: визначення ліквідаційної ціни продукції фірми і найменші маргінальні витрати на ресурси.
4. Аналіз маргінальної продуктивності.
5. Еластичність попиту і пропозицій, виробничих функцій.
Тема 1.20. Застосування диференціального числення функції кількох змінних в економічному аналізі
1. Виробничі функції кількох змінних і граничний аналіз.
2. Частинні граничні витрати, дохід і прибуток.
3. Максимізація прибутку і мінімізація витрат.
4. Частинні еластичності функції та їх економічна інтерпретація.
Література:
[1], т. І, с.210-212, 233-236, 251-252.
[2], с. 397-400, 473-477.
[3], с.234-250, 270-280, 365-368.
Задачі, рекомендовані до розв’язання:
[3], с.248, № 6.51-6.53.
Питання для самоконтролю
1. Граничні витрати, дохід і прибуток.
2. Максимізація прибутку і маргінальний аналіз.
3. Аналіз витрат: визначення ліквідаційної ціни продукції фірми і найменші маргінальні витрати на ресурси.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.