Навчально-методичний посібник для організації самостійної та індивідуальної роботи з дисципліни "Вища математика" (частина І), страница 11

6. При виготовленні комплектів меблів чотирьох видів витрати матеріалів, робочої сили й електроенергії задаються такою таблицею (в умовних одиницях). Обчислити загальну потребу матеріалів y₁, робочої сили y₂ і електроенергії y₃ для виготовлення заданої кількості комплектів меблів кожного виду x₁ =10, x₂ = 5, x₃ =  2, x₄ = 4.

Ресурси	Витрата на один комплект меблів кожного виду
	1	2	3	4
Матеріали Робоча сила Електроенергія	2 2.3 1.6	4 2 3	1 2.5 0.5	2.5 1.5 1

7.  Виконати розрахунок заробітної плати, що припадає на кожне замовлення при виробництві різноманітних виробів, користуючись даними таких таблиць:

	Витрати робочого часу на кожному з робочих місць
Виріб	1	2	3	4
А	1	2.8	1.5	2.6
В	2.3	3.5	2.7	1.9
С	1.5	2.3	3.1	1.4

	Кількість виробів					Робоче місце		Погодинна заробітна плата
Замов-лення	A	B	C			1	2.20
K	4	5	7			2	1.95
L	4	6	2			3	1.75
M	3	0	3			4	2.35

8. Обчислити визначники:

,        .

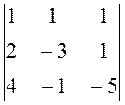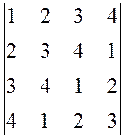9. З¢ясувати, чи існує матриця, обернена до матриці

,

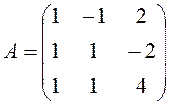і якщо існує, знайти її. Виконати перевірку: .

Розділ 3. ЗАГАЛЬНА ТЕОРІЯ СИСТЕМ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ

1.  Розв’язання систем лінійних рівнянь за допомогою правила Крамера.

2.  Розв’язання систем лінійних рівнянь за допомогою оберненої матриці.

3.  Розв’язання систем методом Гаусса.

4.  Розв’язання систем методом Жордана-Гаусса.

5.  Розв’язання економічних прикладів.

Після опрацювання розділу на практичних заняттях студент повинен

знати: основні поняття і положення лінійної алгебри (системи m рівнянь з n невідомими, сумісність і несумісність, визначеність і невизначеність системи рівнянь, ранг матриці та його обчислення, теорема Кронекера-Капеллі; методи розв’язання систем лінійних рівнянь: методи Гауса і Жордана-Гаусса, метод оберненої матриці, правило Крамера; однорідна система рівнянь та проблема її сумісності);

вміти: обчислювати ранг матриці, досліджувати систему на сумісність, розв’язувати вказаними способами системи лінійних рівнянь.

Література:

[1], т. І, с. 99-117.

[2], с. 129-152.

[3], с. 31-64.

Рекомендації до розв’язання типових прикладів розділу 3

3.1. Розв’язати систему лінійних рівнянь за правилом Крамера.

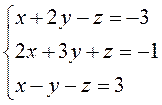
Складемо матрицю системи рівнянь, обчислимо визначник системи та додаткові визначники:

 

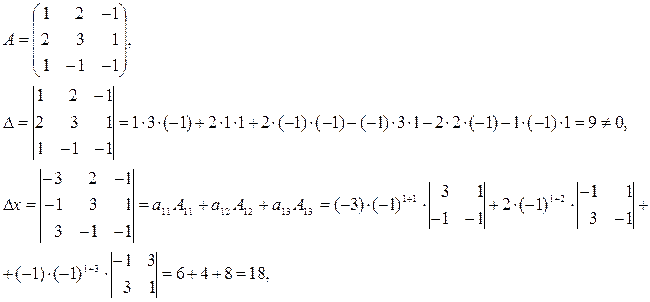
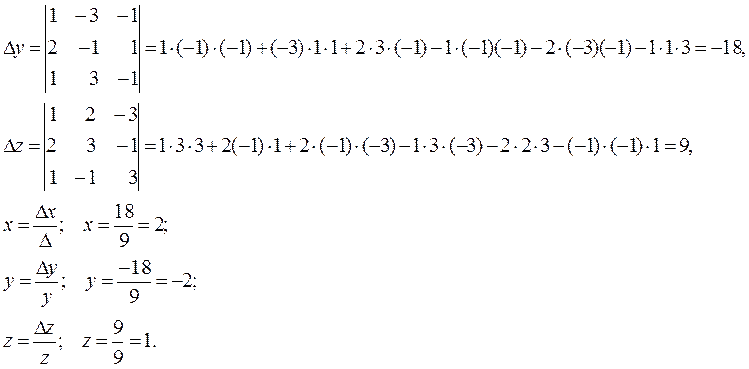
Відповідь: х = 2 ; y = -2 ; z = 1.

3.2. Розв’язати систему лінійних рівнянь, подану в прикладі 1, за допомогою оберненої матриці.

При розв’язуванні попереднього прикладу ми склали матрицю системи А і обчислили визначник . Визначник матриці А не дорівнює нулю, тому матриця А має обернену. Обчислимо алгебраїчні доповнення всіх елементів матриці:

,

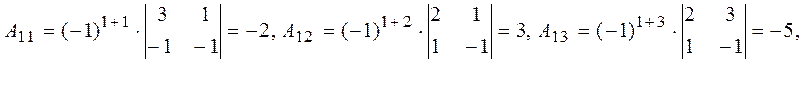
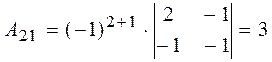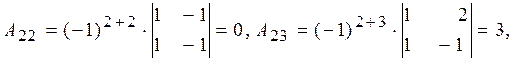
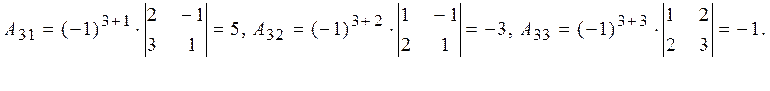
Знайдемо обернену матрицю

.

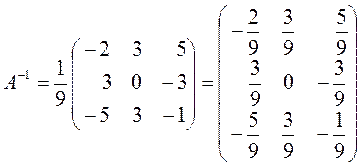Тоді

  .

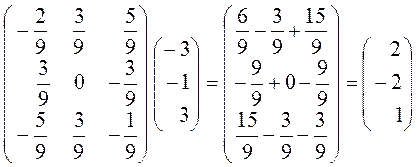Відповідь:

3.3. Розв’язати систему лінійних рівнянь, подану у прикладі 1, методом Гаусса:

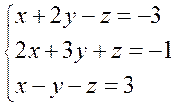
Виключаємо невідоме х із другого і третього рівнянь

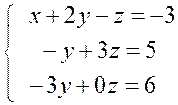
y= – 2

3 z = 5 + y; 3z = 3; z = 1

x = – 3 – 2y + z; x = – 3 – 2 (–2) + 1 = 2

Таким чином, x = 2, y = -2, z = 1.

Відповідь: x = 2, y = -2, z = 1.

3.4. Розв’язати систему лінійних рівнянь методом Гаусса:

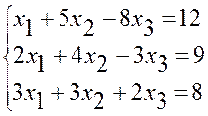
Виключаємо невідоме х₁ із другого і третього рівнянь

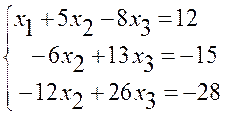
Ділимо друге рівняння на (-6) і виключаємо невідоме х₂ з третього рівняння

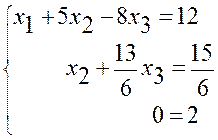
Розглянувши третє рівняння, робимо висновок, що система рівнянь не має розв’язків (система лінійних рівнянь несумісна).

3.5. Розв’язати систему рівнянь методом Гаусса

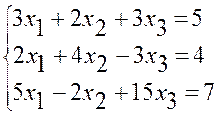
Ділимо перше рівняння на 3 і виключаємо невідоме х₁ з другого і третього рівнянь