Розв’язання.
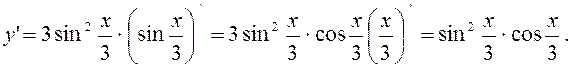
7.10. y=ln(x2+5) ; y’-?
Розв’язання.
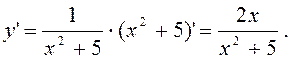
7.11.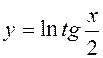 
; y’-?
Розв’язання.
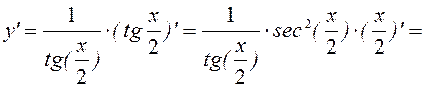
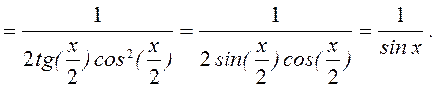
7.12. 
; y’-?
Розв’язання.
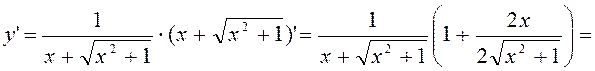
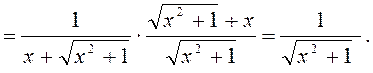
7.13. Знайти похідну
функції 
.
Розв’язання. Прологарифмуємо обидві частини рівняння:
Продиференціюємо обидві частини одержаного співвідношення по х, оскільки y=y(x),то
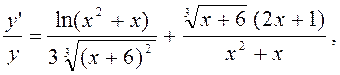
звідси
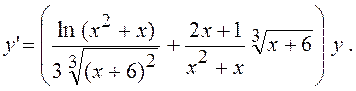
7.14. Знайти y’x
з рівняння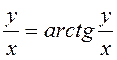 
Розв’язання. Рівняння визначає у як неявну функцію від х. Продиференціюємо обидві частини по х:
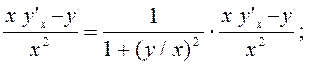
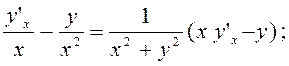
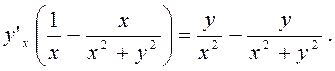
Звідси
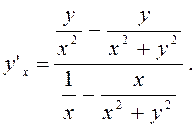
Після перетворення правої частини маємо
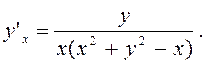
За наведеними вище правилами знаходять і похідні вищих порядків, при цьому слід пам”ятати, що похідна n-го порядку –це похідна від похідної (n-1)-го порядку, тобто
y(n) =(y(n-1))’,n=2,3,…
7.15. Знайти y'', якщо y=cosx2.
Розв’язання.
y’=-2xsinx2;
y”=-2(sinx2+2x2cosx2).
7.16. Скласти рівняння дотичної до кривої y=arcsinx в точці її перетину з віссю OX.
Розв’язання.
Знайдемо координати точки перетину кривої з віссю ОХ:
y=arcsinx=0, x0=0.
Обчислимо значення y’(x) при одержаному значенні змінної:
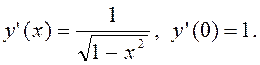
Підставимо у рівняння дотичної y-y0=y’(x0)(x-x0)одержані значення
Рівняння дотичної буде мати вигляд y=x.
Якщо функція диференційовна в точці х, тобто має в цій точці скінченну
похідну y’,то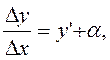 
де a®0 при Dх®0. Звідси Dy=y’Dx+ a Dx.
Головна частина приросту функції Dy, лінійна відносно Dx, називається диференціалом і позначається dy : dy=y'Dx, або dy=y'dx. Справедлива формула: Dy » dy або
f(x+Dx)» f(x)+f'(x)Dx, яка використовується в наближених обчисленнях.
7.17. Знайти dy, якщо y=x2tg2x.
Розв’язання.
.
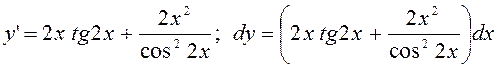7.18. Знайти
диференціал при x=9 функції 
і Dx=-0,06.
Розв’язання.
Знайдемо похідну функції y'(x)
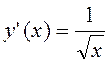
Обчислимо значення y’(x) при x=9
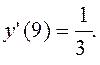
Знайдемо значення диференціала dy=y'(x0)Dx=-0,02 .
7.19. Знайти
наближене значення функції y=
при x=1,03.
Розв’язання.
Визначимо значення x0 і знайдемо Dx:
x0=1; Dx=x-x0=0,03.
Визначимо значення функції y(x) при x=x0:
y(1)=1.
Знайдемо похідну функції y’(x) і її значення при x=x0:
; y’(1)=-4.
Обчислимо диференціал функції dy при x=x0:
dy=y'(x0)Dx=-0,12.
Визначимо наближене значення функції y(x) при x=1,03 з відношення y(x)» y(x0)+dy(x0);
y(1,03)» 0,88.
7. 20. Обчислити дані границі за правилом Лопіталя:
1) 
.
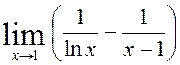Розв’язання. Маємо невизначеність виду ∞–∞. Перетворимо функцію
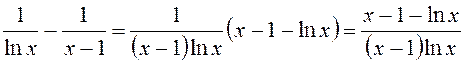, маємо:
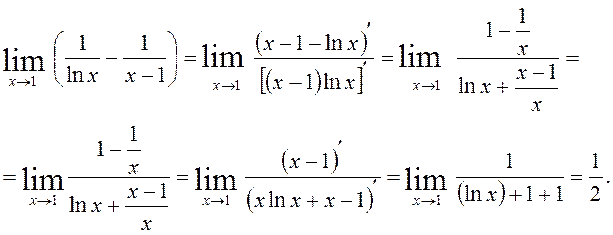
2) 
.
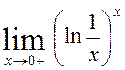Розв’язання.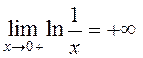
, тут розглядається границя праворуч,
оскільки 
невизначений для х≤ 0.
Маємо невизначеність виду ∞0. Виконаємо перетворення:
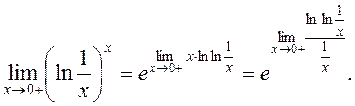
Зробимо заміну змінної, поклавш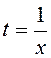и 
. При 
:
.
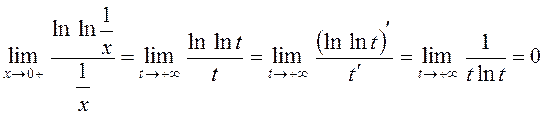Остаточно
.
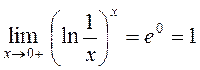7.21. Знайти частинні
похідні першого та другого порядків функції 
.
Розв’язання.
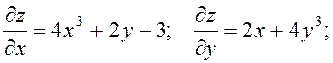
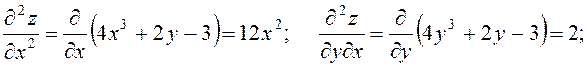
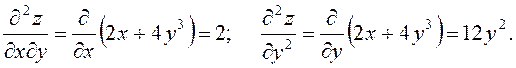
7.22. Знайти значення
частинних похідних в точці Р0 (0;1) функції 
.
Розв’язання. Знаходимо спочатку частинні похідні,
використовуючи формулу диференціювання складної функції 
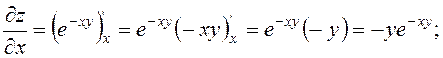
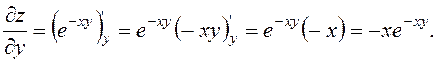
Підставляючи координати точки Р0, одержимо
, 
.
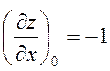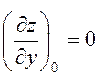7.23. Знайти частинну похідну по z від функції трьох змінних
.
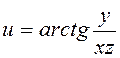Розв’язання. За правилом диференціювання складної функції, вважаючи x та y постійними, одержимо
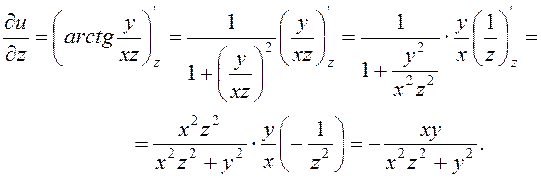
7.24. Довести, що функція 
задовольняє рівнянню
.
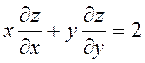Розв’язання. Знаходимо частинні похідні:
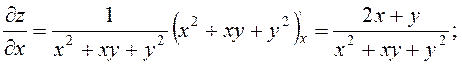
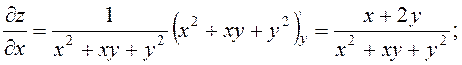
Підставляємо 
і 
в дане
рівняння:
, 
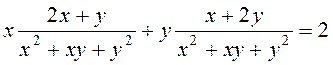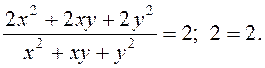
7.25. Знайти повний
диференціал функції 
Розв’язання. Знаходимо частинні похідні:
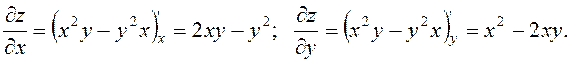
7.26. Дано: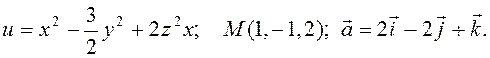 
Знайти: 1)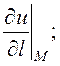 
2) 
Розв’язання. 1) Знаходимо похідну за напрямком:
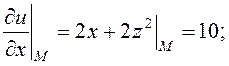
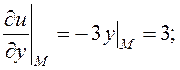
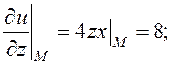
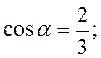
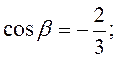
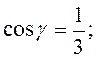
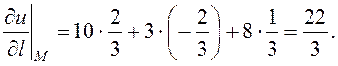
2) Знаходимо градієнт функції в точці М:
7.27.Розрахувати еластичність даних функцій і знайти значення показника еластичності для заданих x
а) y = x3 + 1, x = 1, x = 5;
б) y = e5x , x = 1, x = 0, x = 2;
в) y = 5lnx, x = 10, x = e, x = e4.
|
Ex(y) = |
Розмір Ex(y)при заданому значенні x називають показником або коефіцієнтом еластичності. Еластичність щодо x є наближений процентний приріст функції (підвищення або зниження), що відповідає збільшенню незалежної змінної на 1%.
а)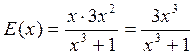 
; 
; 
;
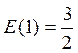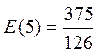б)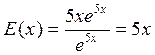 
; 
; 
; 
;
в)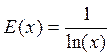 
; 
; 
; 
.
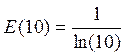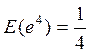7.28. Витрати виробництва x одиниць однорідної продукції виражені рівнянням: y = x3 - 3x2 + 10x. Необхідно знайти: а) обсяг виробництва, при якому середні витрати будуть мінімальними; б) граничні витрати при обсягу виробництва х=4.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
y¢