знати: основні поняття векторної алгебри (вектор, дії з векторами, координати вектора, скалярний, векторний, мішаний добутки векторів, базис векторного простору), економічну інтерпретацію основних понять та дій векторної алгебри; основні поняття аналітичної геометрії (рівняння лінії на площині, рівняння лінії 2-го порядку на площині, рівняння площини та прямої у просторі, рівняння поверхні другого порядку), інтерпретацію основних ліній та поверхонь як математичних моделей економічних процесів;
вміти: виконувати дії з векторами, в тому числі, з використанням скалярного, векторного, мішаного добутків векторів, розкладати вектор за базисом; складати рівняння прямої на площині у різних виглядах, рівняння площини та прямої у просторі у різних виглядах, знаходити відстань від точки до прямої, від точки до площин , досліджувати взаємне розташування прямих та площин.
Рекомендована література:
[1], т. І, с. 125-139, с. 142-157, с.162-169.
[2], с. 227-238, с.239-250, с.269-291.
[3], с. 82-115, с. 116-170.
Рекомендації до розв’язання типових прикладів розділу 5
5.1.Знайти довжину вектора ![]() , якщо
відомі координати точок А(2; -1), В(-3; 0), С(5; -2).
, якщо
відомі координати точок А(2; -1), В(-3; 0), С(5; -2).
Розв¢язання.
1)
Якщо вектор ![]() має своїм початком точку А(х1;
у1; z1), а кінцем точку В(х2;
y2; z2), то координати вектора
має своїм початком точку А(х1;
у1; z1), а кінцем точку В(х2;
y2; z2), то координати вектора ![]() обчислюються за правилом:
обчислюються за правилом:
![]()
2)
Якщо ![]() то
то
![]()
3)Якщо ![]() то довжина
то довжина ![]() . Тоді
. Тоді![]()
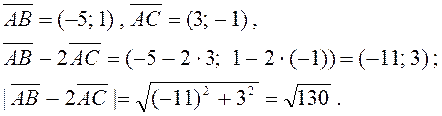
5.2.Знайти орт вектора ![]()
Розв’язання.
![]() ,
,
Тоді 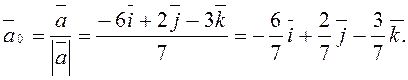
Відповідь:![]()
5.3.У трикутнику з вершинами А(2;-1;3), В(-2;2;5), С(1;2;3) знайти кут при вершині А.
 Розв¢язання.
Розв¢язання.
![]() тоді
тоді
cosj=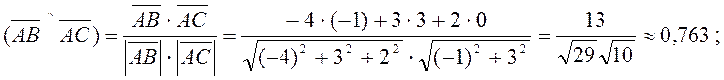
j » arccos 0,763 »40°18¢.
5.4.Знайти точку D так, щоб чотирикутник АВСD був паралелограмом, якщо
А(-2; 0), В(1; -3), С(2; 5).
Розв¢язання.
 |
Якщо АВСD- паралелограм, то ![]() а два
вектори рівні, якщо рівні відповідні координати. Позначимо через х,у невідомі координати точки D. Тоді
а два
вектори рівні, якщо рівні відповідні координати. Позначимо через х,у невідомі координати точки D. Тоді
![]()
З умови рівності координат маємо:
2 –х = 3, 5-у =-3, звідси х = -1, у = 8.
Отже, одержали координати точки D (-1; 8).
5.5.Знайти точку С на осі Оy так, щоб кут АВС був прямим, якщо задані точки А(6; 4), В(-2; 5).
Розв¢язання.
Введемо (0; у) –координати точки С. Необхідною та
недостатньою умовою ортогональності векторів ![]() є рівність
нулю їх скалярного добутку:
є рівність
нулю їх скалярного добутку: ![]() Скористуємося
формулою для обчислення скалярного добутку:
Скористуємося
формулою для обчислення скалярного добутку:
![]() де
де ![]()
Тоді маємо 8×2 -1×(у-5) =0, 16 – у + 5 =0, у = 21.
Отже, маємо С(0; 21).
5.6.Розкласти
вектор ![]() по векторах
по векторах ![]()
![]() та
та
![]()
Розв¢язання.
Розкласти вектор ![]() по
векторах
по
векторах ![]() означає представити його у вигляді
лінійної комбінації
означає представити його у вигляді
лінійної комбінації
![]() - поки ще невідомі числа. Переходячи до
координат, одержимо
- поки ще невідомі числа. Переходячи до
координат, одержимо
![]()
У результаті приходимо до системи рівнянь
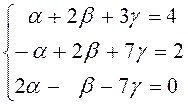 , вирішуючи яку,
знаходимо:
, вирішуючи яку,
знаходимо:
![]()
Звідси ![]()
5.7. Скласти рівняння прямої, що проходить через точки М(-1; 3) та N(2; 5)
Розв’язання.
Скористаємося рівнянням прямої на площині, що проходить через точки М1(х1; у1)та М2(х2; у2):
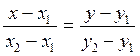 .
.
Підставляючи в це рівняння наші дані, одержуємо
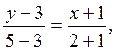 або
або 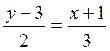 .
.
Рівняння має вигляд 2х –3у +11= 0.
Корисно перевірити, що рівняння складено вірно. Для цього достатньо показати, що координати точок М та Nзадовольняють рівнянню прямої. Дійсно, рівності
2(-1)-3·3+11= 0, 2·2- 3·5 +11=0 виконуються тотожно.
5.8. Дані вершини трикутника: M(0;1); N(6;5) та С(12;-1). Скласти рівняння висоти трикутника, проведеної з вершини С.
Розв’язання.
 |
Скористаємося рівнянням прямої на площині, яка
проходить через точку C(x0; y0)та має вектор
нормалі ![]() :
:
A(х-х0) + В(у-у0) =0.
Зі схематичного
рисунка видно, що в якості вектора нормалі прямої СК можна взяти вектор ![]() . Тоді маємо:
. Тоді маємо:
6(x-12) + 4(у+1) =0, звідки одержуємо 3х +2у –34 =0.
5.9. Скласти рівняння прямої, що проходить через точку М(-2; -5) і паралельно прямій 3х +4у +2 =0.
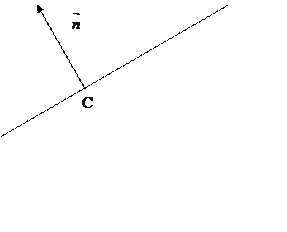 Розв’язання.
Розв’язання.
З схематичного рисунка бачимо, що вектор нормалі ![]() даної прямої є і вектором нормалі шуканої
прямої. Тоді, застосувавши рівняння з попередньої задачі, маємо:
даної прямої є і вектором нормалі шуканої
прямої. Тоді, застосувавши рівняння з попередньої задачі, маємо:
3(х+2) + 4(у+5) =0, звідки 3х + 4у +26 =0.
5.10. Дані вершини трикутника А(-2; -3), В(5; 4) та С(-1; 2). Скласти рівняння медіани АМ.
Розв’язання.
Точка М –середина сторони ВС, тому
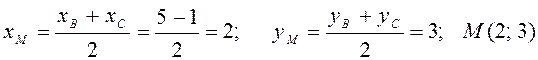 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.