Матрицею називається упорядкована таблиця чисел:
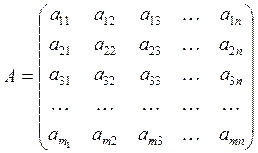 - матриця розміром mxn, аij – елементи матриці, де i -номер
рядка матрицi (i =1,…,m), j - номер стовпця матрицi (j=1,…,n), на
перетинi яких знаходиться відповідний елемент.
- матриця розміром mxn, аij – елементи матриці, де i -номер
рядка матрицi (i =1,…,m), j - номер стовпця матрицi (j=1,…,n), на
перетинi яких знаходиться відповідний елемент.
1)Якщо кiлькiсть рядкiв матрицi m не дорiвнює кiлькостi її стовпцiв n, то матриця називається прямокутною.
2) Матриця, в якій кількість n рядків дорівнює кількості стовпців, називається квадратною n-го порядку.
3) Нульовою матрицею називається матриця, в якій всі елементи дорівнюють нулю.
4) Матрицю, що має тiльки один рядок (стовпець), називають вектором-рядком (вектором-стовпцем).
5) Дiагональна матриця має вигляд:
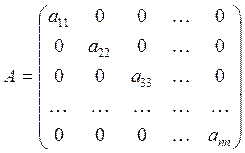 .
.
6) Одинична матриця n-го порядку:
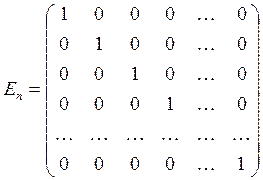
7) Якщо в матрицi А помiняти мiсцями вiдповiднi рядки i стовпцi, то одержимо матрицю АT, яка називається транспонованою матрицею по вiдношенню до матрицi А.
1) Сумою двох матриць А і В рівних розмірів (mхn) називається матриця С того ж розміру, елементи якої сij дорівнюють сумі відповідних елементів матриць А і В.
2) Добутком матриці на число називається матриця, елементи якої одержані з даної множенням усіх її елементів на це число.
3) Добутком матриць А і В називається матриця С, елемент ![]() якої дорівнює сумі попарних добутків
елементів i-того рядка матриці А на відповідні елементи j-го стовпця
матриці В.
якої дорівнює сумі попарних добутків
елементів i-того рядка матриці А на відповідні елементи j-го стовпця
матриці В.
Визначником 2-го порядку, складеним для квадратної матриці А=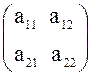 , називається число
, називається число
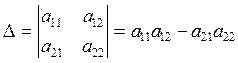 .
.
Визначником 3-го порядку, складеним для квадратної матриці
А=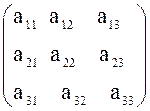 , називається число
, називається число 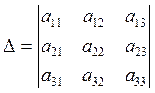 =
=
![]() (правило трикутника).
(правило трикутника).
Схематичне зображення правила трикутника:
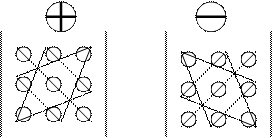 |
Основні властивості визначників
Визначник не зміниться, якщо його рядки поміняти місцями з відповідними стовпцями.
При переставленні місцями будь-яких двох рядків визначник змінює знак на протилежний.
Якщо відповідні елементи двох рядків визначника рівні або пропорціональні, то визначник дорівнює нулю.
Якщо всі елементи якого-небудь рядка дорівнюють нулю, то визначник дорівнює нулю.
Загальний множник всіх елементів рядка можна винести за знак визначника.
Якщо кожний елемент деякого рядка визначника є сумою двох доданків, то цей визначник дорівнює сумі двох визначників, в одному з яких у тому ж рядку стоять перші доданки, а у другому – другі. Інші рядки у обох визначників однакові та співпадають з відповідними рядками даного визначника.
Величина визначника не зміниться, якщо до елементів одного рядка додати відповідні елементи іншого рядка, помножені на одне й те ж саме число.
Мінор Mij елемента аij визначника – це визначник, який одержано з даноговикресленням і-го рядка та j-го стовпця, на перетині яких знаходиться елемент.
Алгебраїчне доповнення Аij
елемента аij
– це мінор Мij цього елемента, взятий з відповідним знаком за
схемою 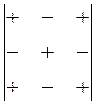 .
.
Теорема (про розкладання визначника за елементами рядка або стовпця). Визначник дорівнює сумі добутків елементів будь-якого рядка (стовпця) на їхні алгебраїчні доповнення.
Система т лінійних рівнянь з п невідомими має вигляд:
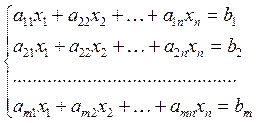 (1)
(1)
де ![]() - дійсні числа, які називають
коефіцієнтами системи,
- дійсні числа, які називають
коефіцієнтами системи, ![]() , i =1,…,m - вільні члени
або праві частини рівнянь,
, i =1,…,m - вільні члени
або праві частини рівнянь, ![]() , j=1,…,n -
невідомі. Якщо n=m, то система називається квадратною. Запис
системи (1) в матричному вигляді:
, j=1,…,n -
невідомі. Якщо n=m, то система називається квадратною. Запис
системи (1) в матричному вигляді:
![]() ,
(1’)
,
(1’)
де 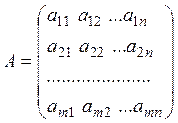 – матриця системи, складена із
коефіцієнтів при невідомих,
– матриця системи, складена із
коефіцієнтів при невідомих, 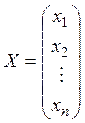 - вектор-стовпець
невідомих,
- вектор-стовпець
невідомих,
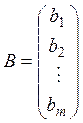 - вектор-стовпець вільних членів.
- вектор-стовпець вільних членів.
Розв’яком системи (1) називається
така сукупність n чисел ![]() , при
підстановці яких кожне рівняння системи перетворюється на вірну рівність.
, при
підстановці яких кожне рівняння системи перетворюється на вірну рівність.
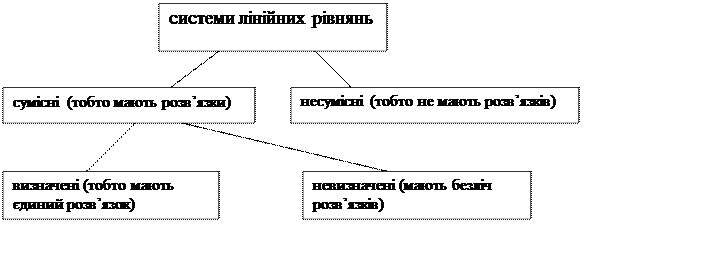 |
Розглянемо систему трьох лінійних рівнянь з трьома невідомими:
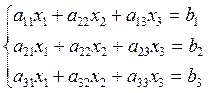 (2)
(2)
Визначник 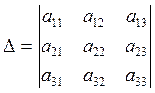 називається
визначником системи (2).
називається
визначником системи (2).
Складемо визначники:
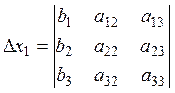 ,
, 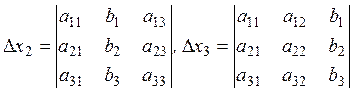 .
.
Теорема (Крамера). Якщо визначник системи (2) не дорівнює нулю, то система має єдиний розв’язок, який знаходиться за формулами:
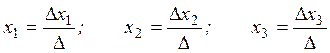 .
.
Матрицю А-1 називають оберненою по відношенню до квадратної матриці А, якщо
![]() , де Е – одинична матриця.
, де Е – одинична матриця.
Для того, щоб квадратна матриця А мала
обернену, необхідно і достатньо, щоб визначник ![]() матриці А не дорівнював
нулю.
матриці А не дорівнював
нулю.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.