Математика \ Высшая математика

Навчально-методичний посібник для організації самостійної та індивідуальної роботи з дисципліни "Вища математика" (частина І), страница 27

1)	2)
3)	4)
5)	6)
7)	8)
9)	10)
11)	12)
13)	14)

11. Знайти повні диференціали вказаних функцій

1)	2)
3)	4)
5)	6)
7)	8)
9)	10)
11)	12)
13)	14)
15)	16)
17)	18)
19)	20)

12. Знайти частинні похідні 2-го порядку вказаних функцій

1)	2)
3)	4)
5)	6)
7)	8)
9)	10)
11)	12)
13)	14)

13. Знайти градієнт функції в точці М та похідну функції за напрямком вектора в точці М:

1)
2)
3)
4)
5)
6)
7)
8)
9)
10)

14. Розрахувати еластичність даних функцій і знайти значення показника еластичності для заданих x:

а) y = log ₂5x, x = 2, x = 5;

б) y = x⁴ + x² + 1, x = 0, x = 3.

15. Крива повних витрат має вигляд P = 3x² + 7lnx. Визначити криву граничних витрат.

16. Функція середніх витрат має вигляд: S = 5x³+ 4x² - 12x, де x ‑ кількість одиниць продукції. Який вид будет мати функція повних витрат? Чому дорівнює обсяг виробництва, при якому середні витрати мінімальні?

17. Фірма реалізує x одиниць продукції на місяць. Функція, що визначає прибуток фірми, має вигляд 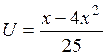. Знайти а) залежність між питомою ціною і кількістю одиниць продукції;

б) умови, при яких прибуток буде мінімальним.

Глава ІІІ. ІНДИВІДУАЛЬНІ ДОМАШНІ ЗАВДАННЯ (ІДЗ) З ДИСЦИПЛІНИ «ВИЩА МАТЕМАТИКА» ДЛЯ СТУДЕНТІВ ДЕННОЇ ФОРМИ НАВЧАННЯ ТА РЕКОМЕНДАЦІЇ ДО ЇХ ВИКОНАННЯ

ІДЗ № 1

Мета роботи: відпрацювання практичних навичок розв’язання систем лінійних рівнянь та дослідження їх на сумісність.

Рекомендації до виконання ІДЗ №1: слід звернути увагу на умови, за яких можна застосовувати різні методи розв’язання систем, та на окремі випадки використання теореми Кронекера-Капеллі. Перед виконанням завдання рекомендується опрацювати задачі 3.1-3.7 даного посібника з глави ІІ.

Література:[1], т. І, с. 99-117, [2], с. 129-152, [3], с. 31-64.

Зміст ІДЗ № 1

(N – номер варіанта)

1. Розв’язати систему лінійних рівнянь за правилом Крамера, матричним методом, методом Гаусса, методом Жордана-Гаусса:

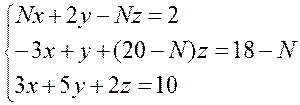
2. Розв’язати систему лінійних рівнянь методом Гаусса:

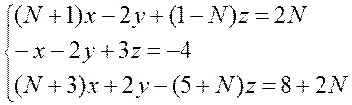
3. Розв’язати систему лінійних рівнянь методом Гаусса:

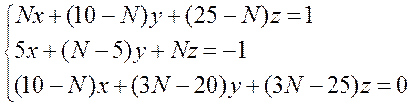
4. Дослідити систему лінійних рівнянь на сумісність:

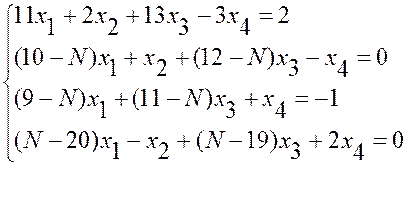
ІДЗ № 2

Мета роботи: відпрацювання практичних навичок розв’язання типових задач з векторної алгебри.

Рекомендації до виконання ІДЗ №2: слід звернути увагу на основні формули векторної алгебри. Особливу увагу необхідно приділити поняттям «лінійна незалежність векторів», «координатний базис», «розкладання вектора за базисом» (останнє завдання). В останньому завданні отриману в процесі розв¢язання лінійну систему можна розв¢язувати будь-яким способом (за вибором студента). Перед виконанням завдання рекомендується опрацювати задачі 5.1-5.6 даного посібника з глави ІІ.

Література: [1], т. І, с. 125-139, [2], с. 227-238, [3], с. 82-115.

Зміст ІДЗ № 2

1. Дані точки А(N; 3; -1); В(7; 0; 1), С(2; -N; 4),D(4; 2; 5)

Знайти:

3) довжину векторів ;