Формула для знаходження оберненої матриці: 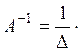
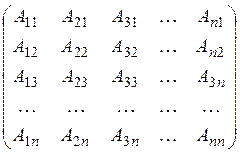 , де
, де ![]() -
визначник матриці А,
-
визначник матриці А, ![]() - алгебраїчні
доповнення елементів аij.
- алгебраїчні
доповнення елементів аij.
Матричний метод: Розв’язок квадратної системи (1’), визначник якої не дорівнює нулю, знаходиться за формулою:
![]() .
.
Дві системи рівнянь називаються рівносильними, якщо вони мають однакову множину розв’язків. Від даної системи до рівносильної їй можна прийти за допомогою еквівалентних перетворень систем рівнянь, до яких відносяться множення обох частин рівнянь на ненульове число та складання відповідних частин рівнянь системи.
Метод Гаусса (метод послідовних виключень) полягає в тому, що за допомогою елементарних перетворень система рівнянь приводиться до рівносильної системи ступінчастого (або трикутного) вигляду, з якої послідовно, починаючи з останніх за номером змінних, знаходяться усі інші змінні.
Метод Жордана-Гаусса (метод повного виключення) полягає в тому, що за допомогою елементарних перетворень система рівнянь приводиться до рівносильної системи діагонального вигляду.
Розглянемо матрицю
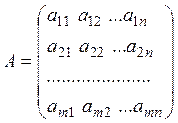 .
.
Виділимо в ній будь-які k рядків та k стовпців. Елементи, розміщені на їх перетині, утворюють квадратну матрицю k –го порядку; визначник цієї матриці називається мінором k–го порядку матриці А.
Рангом r(A) матриці Aназивається найбільший порядок відмінних від нуля мінорів цієї матриці.
При знаходженні рангу користуються тим , що ранг не змінюється при виконанні елементарних перетворень над матрицею, до яких відносяться такі операції:
1) переставлення місцями будь-яких двох рядків (стовпців);
2) множення усіх елементів будь-якого рядка (стовпця) на відмінне від нуля число;
3) додавання до усіх елементів деякого рядка (стовпця) матриці відповідних елементів іншого рядка (стовпця), помножених на одне й те саме число;
4) відкидання нульового рядка (стовпця).
2. Матриця 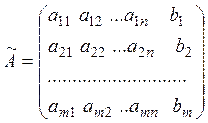 називається розширеною
матрицею системи (1).
називається розширеною
матрицею системи (1).
Теорема (Кронекера-Капеллі). Система лінійних рівнянь (1) сумісна тоді і лише тоді, коли ранг
розширеної матриці системи дорівнює рангу матриці системи: ![]() .
.
Перед виконанням завдання № 1 рекомендується опрацювати приклади 3.1-3.7 глави ІІ.
§4. ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ ДО ЗАВДАННЯ №2
Література: [1], т. І, с. 125-139, [2], с. 227-238, [3], с. 82-115.
Вектор ![]() – це напрямлений
відрізок, довжина якого називається модулем вектора (пишуть
– це напрямлений
відрізок, довжина якого називається модулем вектора (пишуть ![]() ).
).
Два вектори ![]() і
і ![]() називаються протилежними, якщо для
них виконується рівність
називаються протилежними, якщо для
них виконується рівність ![]() .
.
Два колінеарних (паралельних) вектора ![]() і
і ![]() відрізняються
скалярним множником
відрізняються
скалярним множником ![]() .
.
Розкладання вектора за координатними осями Ox, Oy, Ozзаписується
у вигляді ![]() , або
, або ![]() , де x, y, z–
проекції вектора
, де x, y, z–
проекції вектора ![]() на Ox,
Oy, Oz;
на Ox,
Oy, Oz;
![]() –
одиничні вектори (орти), які співпадають за напрямком з цими осями. Проекції x, y, zназиваються
координатами вектора.
–
одиничні вектори (орти), які співпадають за напрямком з цими осями. Проекції x, y, zназиваються
координатами вектора.
Довжина вектора ![]() знаходиться
за формулою
знаходиться
за формулою ![]() .
.
Якщо α, β, γ – кути між вектором ![]() і осями Ox,
Oy, Oz,
то cosα,
cosβ, cosγ називаються напрямними косинусами
вектора
і осями Ox,
Oy, Oz,
то cosα,
cosβ, cosγ називаються напрямними косинусами
вектора ![]() і обчислюються за формулою
і обчислюються за формулою 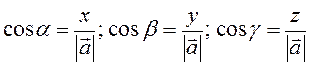 .
.
Якщо відомі координати точок А(x1, y1, z1) і В(x2, y2, z2), то ![]() .
.
Якщо два вектори ![]() = (x1, y1, z1) і
= (x1, y1, z1) і ![]() =(x2, y2, z2) колінеарні, то їхні координати пропорційні, тобто
=(x2, y2, z2) колінеарні, то їхні координати пропорційні, тобто
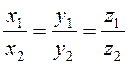 .
.
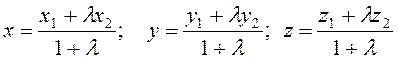 .
.
Скалярним добутком двох векторів ![]() і
і ![]() називається число, яке дорівнює добутку
довжин цих векторів на косинус кута між ними:
називається число, яке дорівнює добутку
довжин цих векторів на косинус кута між ними:
![]() .
.
Якщо вектори задані своїми координатами, то
![]() .
.
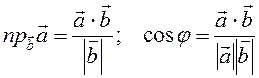 .
.
Упорядковану сукупність n
дійсних чисел називають n-вимірним вектором ![]() = (a1,a2,…an), числа
= (a1,a2,…an), числа ![]() –
координати вектора.
–
координати вектора.
Сукупність усіх n-вимірних векторів називається n-вимірним векторним простором. Позначення Rn.
Система векторів ![]() називається
лінійно залежною, якщо існують такі не всі рівні нулю числа α1,
α2,..., αm, що має місце співвідношення
називається
лінійно залежною, якщо існують такі не всі рівні нулю числа α1,
α2,..., αm, що має місце співвідношення
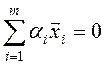 .
.
У протилежному випадку дана система векторів називається лінійно незалежною, тобто указана рівність має місце лише у випадку, коли всі αi =0.
Будь-які nлінійно незалежних векторів утворюють базис n-вимірного простору.
Нехай вектори ![]() утворюють базис в Rn. Тоді
будь-який вектор
утворюють базис в Rn. Тоді
будь-який вектор ![]() можна розкласти за цим базисом,
тобто
можна розкласти за цим базисом,
тобто
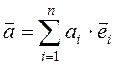 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.