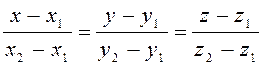 .
.
Підставляючи наші дані,одержуємо:
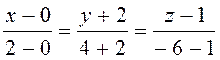 або
або 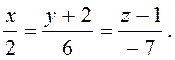
 5.25.
Скласти рівняння прямої, що проходить через точку М0(1,-1,2)
перпендикулярно площині х-2у-1=0.
5.25.
Скласти рівняння прямої, що проходить через точку М0(1,-1,2)
перпендикулярно площині х-2у-1=0.
Розв’язання.
В якості напрямного вектора візьмемо нормальний вектор ![]() заданої площини.
заданої площини.
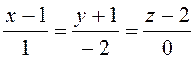 .
.
Тут 0 у знаменнику означає, що пряма перпендикулярна осі OZ.
5.26.Знайти величину кута j між площинами 2x+3y-5z+2=0 та 3x-4y+2z-7=0.
Розв’язання.Оскільки
кут між площинами дорівнює куту між їх нормальними векторами ![]() то
то
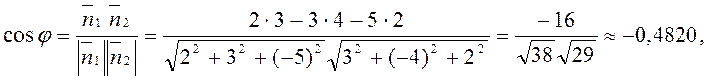
j»arccos(-0,4820) »118,82°.
Відповідь: j »118,82°.
5.27. Знайти
величину кута a між прямою 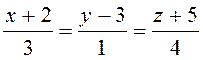 та
площиною
та
площиною
2х – у + 3z+ 5=0.
Розв’язання. ![]() - напрямний вектор
прямої,
- напрямний вектор
прямої, ![]() -вектор нормалі площини, тому
-вектор нормалі площини, тому
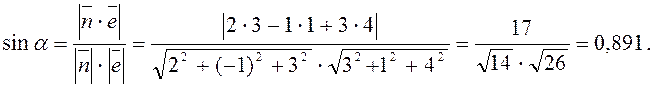
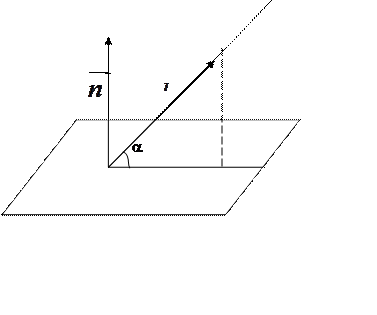 |
Таким чином, a=arcsin 0,891»630.
Відповідь: a »630.
5.28.Знайти відстань від точки К(1,6,3) до площини,що проходить через точки А(4,5,2), В(-1,11,-6) та С(2,-1,3).
Розв’язання.
Складемо рівняння площини, що проходить через три точки:
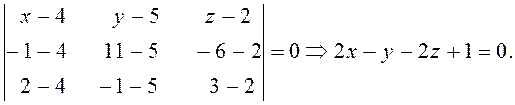
Скористаємося формулою для знаходження відстані d від точки К( x0; y0; z0) до площини Аx +Вy +Сz +D=0:
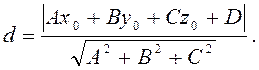
Підставляючи наші дані, маємо:
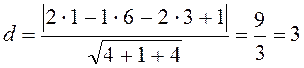 .
.
5.29. Знайти
точку перетину прямої 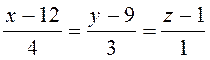 і площини
і площини
3х +5у –z –2=0.
Розв’язання. Перетворивши канонічні рівняння прямої до параметричного виду
х = 4t + 12, y = 3t + 9, z = t +1 і підставивши їх в рівняння площини, знайдемо:
3(4t +12) + 5(3t +9)- (t+1)-2 = 0, звідки 26t=-78, t =-3.
Задані пряма і площина перетинаються в точці з координатами
х= 4×(-3)+12=0; у=3×(-3)+9=0; z=-3+1=-2.
Отже, пряма і площина перетинаються у точці (0;0;-2).
Задачі, рекомендовані до розв’язання на практичних заняттях з розділу 5
1. За даними
векторами ![]() і
і ![]() побудувати
кожен з наступних векторів: 1)
побудувати
кожен з наступних векторів: 1) ![]() +
+ ![]() ;
2)
;
2)![]() –
–![]() ; 3)
; 3) ![]() –
– ![]() ;
4) –
;
4) –![]() –
–![]() .
.
2. Маємо: ![]() Обчислити |
Обчислити |![]()
3. Маємо: |![]() та
|
та
|![]() Визначити |
Визначити |![]()
4. Вектори a і b
взаємно перпендикулярні, причому |![]() |= 5 і |
|= 5 і |![]() |=12.
Визначити |
|=12.
Визначити |![]() | та |
| та |![]() |.
|.
5. Вектори ![]() і
і
![]() утворюють кут j = 60°, причому |
утворюють кут j = 60°, причому |![]() |=5 і |
|=5 і |![]() |=8.
Визначити |
|=8.
Визначити |![]() | та |
| та |![]() |.
|.
6.
Вектори ![]() і
і ![]() утворюють
кут j = 120°, причому |
утворюють
кут j = 120°, причому |![]() |=3
і |
|=3
і |![]() |=5. Визначити |
|=5. Визначити |![]() | та |
| та |![]() |.
|.
7.
Якій умові повинні задовольняти вектори ![]() і
і ![]() щоб мали місце такі співвідношення: 1)|
щоб мали місце такі співвідношення: 1)|![]() |=|
|=|![]() |;
2)|
|;
2)|![]() |>|
|>|![]() |; 3)
|; 3)![]()
8.
Якій умові повинні задовольняти вектори ![]() і
і ![]() ,
щоб вектор
,
щоб вектор ![]() ділив навпіл кут між векторами
ділив навпіл кут між векторами ![]() і
і
![]() .
.
9.
За даними векторами ![]() і
і ![]() побудувати
такі вектори:
побудувати
такі вектори:
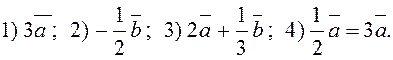
10.
Точка О є центром ваги трикутника АВС. Довести, що ![]()
11. Перевірити колінеарність векторів ![]() ={2; -1; 3} і
={2; -1; 3} і ![]() {-6;
3; -9}. Визначити, який з них довше і у скільки
разів, як вони направлені - в один бік чи в протилежні сторони.
{-6;
3; -9}. Визначити, який з них довше і у скільки
разів, як вони направлені - в один бік чи в протилежні сторони.
12. Визначити, при яких значеннях a,b вектори ![]() =-2i+3j+bk та
=-2i+3j+bk та ![]() =ai-6j+2k колінеарні.
=ai-6j+2k колінеарні.
13. Перевірити та впевнитись, що чотири точки А(3; -1; 2), В(1; 2;-1), С(-1;1;-3), D(5;0;4) служать вершинами трапеції.
14. Маємо точки А(-1; 5; -10), В(5; -7; 8), С(2; 2; -7) та D(5; -4;2). Перевірити і впевнитись, що вектори ![]() та
та
![]() колінеарні; встановити який з них довше і
у скільки разів, як вони направлені
- в один бік чи в протилежні
сторони.
колінеарні; встановити який з них довше і
у скільки разів, як вони направлені
- в один бік чи в протилежні
сторони.
15. Маємо дві вершини А(2; -3;-5), В(-1;3; 2) паралелограма АВСD і точку перетину його діагоналей Е(4; -1; 7).Визначити дві інші вершини цього паралелограма.
16. Маємо три вершини А(3; -4; 7), В(-5; 3; -2) та С(-4; 2; -3) паралелограма АВСD. Знайти його четверту вершину D, протилежну В.
17.
Знайти орт вектора: а) ![]() = (6; -2;
-3); б)
= (6; -2;
-3); б) ![]() = (3; 4; -12).
= (3; 4; -12).
18.
На площині є три вектори ![]() =(3; -2),
=(3; -2), ![]() (-2; 1) та
(-2; 1) та ![]() =(7;
-4). Визначити розклад кожного з цих трьох векторів, приймаючи в якості базису
два інших.
=(7;
-4). Визначити розклад кожного з цих трьох векторів, приймаючи в якості базису
два інших.
19. Маємо три вектори ![]() =(3; -1),
=(3; -1), ![]() (1; -2) та
(1; -2) та ![]() =(-1;
7). Визначити розклад вектора
=(-1;
7). Визначити розклад вектора ![]() за базисом
за базисом ![]()
20.
Маємо три вектори ![]() =(3; -2; 1),
=(3; -2; 1), ![]() =(-1; 1; -2) та
=(-1; 1; -2) та ![]() =(2; 1;
-3). Знайти розклад вектора
=(2; 1;
-3). Знайти розклад вектора ![]() = (11;
-6; 5) за базисом
= (11;
-6; 5) за базисом ![]()
21. Маємо чотири вектори ![]() =(2; 1; 0),
=(2; 1; 0), ![]()
![]() (1; -1; 2),
(1; -1; 2), ![]() =(2; 2;
-1),
=(2; 2;
-1), ![]() (3; 7; -7). Визначити розклад кожного з цих
чотирьох векторів, приймаючи в якості базису останні три.
(3; 7; -7). Визначити розклад кожного з цих
чотирьох векторів, приймаючи в якості базису останні три.
22. Вектори ![]() та
та ![]() утворюють
кут
утворюють
кут 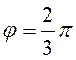 ; знаючи, що |
; знаючи, що |![]() |=3,
|
|=3,
|![]() |=4, обчислити:
|=4, обчислити: ![]()
24. Маємо вектори ![]() Обчислити:
Обчислити: ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.