Навчально-методичний посібник для організації самостійної та індивідуальної роботи з дисципліни "Вища математика" (частина І), страница 2

6.  Поняття оберненої матриці та метод її обчислення.

Література:

[1], т. І, с. 73-89.

[2], с.  82-128.

[3], с. 13-30.

Задачі, рекомендовані до розв’язання:

[3], с. 61, № 1.63-1.66, с. 78-79, № 1.75-1.84.

Питання для самоконтролю

1.  Що називається визначником? Які основні властивості визначників?

2.  Які способи обчислення визначників? Приведіть приклади.

3.  Чому дорівнює основний визначник невизначеної квадратної системи лінійних рівнянь?

4.  Знайдіть добуток матриць: 

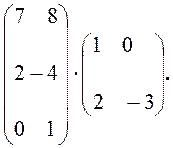
5.  Чи може однорідна лінійна система бути несумісною?

6.  Запишіть вираз 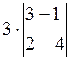 у вигляді одного визначника другого порядку.

7.  Знайдіть добуток матриць: 

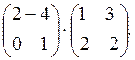
8.  Запишіть одиничну матрицю 4-го порядку.

9.  Якій умові повинна задовольняти матриця, яка має обернену матрицю?

10.Заповнити пусті місця одним з можливих способів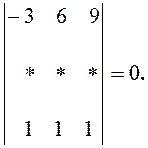

11.Назвіть усі відомі Вам способи обчислення визначника 3-го порядку.

12.Чи будь-яка матриця має визначник? Відповідь пояснити.

13.Якій умові повинна задовольняти матриця, яка має обернену матрицю?

14.Який найбільший ранг може мати матриця розміром 4х2?

15.Обчисліть основний визначник системи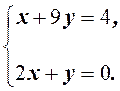

16.Скласти матрицю, транспоновану до матриці .

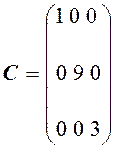17.Заповнити пусті місця будь-яким з можливих способів: = -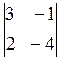

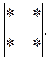
18.Що можна стверджувати щодо сумісності лінійної системи, якщо ранг її розширеної матриці коефіцієнтів дорівнює кількості невідомих системи?

19.Сформулюйте теорему Кронекера-Капеллі.

Результат виконання роботи: складання конспекту, виконання домашнього завдання.

Форма контролю: усне опитування, обговорення питань, перевірка конспекту.

Розділ 3. ЗАГАЛЬНА ТЕОРІЯ СИСТЕМ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ

Тема 1.5. Система m лінійних рівнянь з n невідомими

1.  Поняття системи m рівнянь з n невідомими та запис її у матричній формі.

2.  Сумісність і несумісність, визначеність і невизначеність системи рівнянь.

3.  Ранг матриці та його зв’язок з лінійною незалежністю рядків (стовпців) матриці.

4.  Поняття базисного мінора матриці.

5.  Елементарні перетворення матриці та обчислення за їх допомогою рангу матриці.

6.  Теорема Кронекера-Капеллі.

7.  Методи Гауса і Жордана-Гаусса розв’язування системи рівнянь.

8.  Загальний і базисний розв’язки системи рівнянь.

9.  Лінійна однорідна система рівнянь, фундаментальна система її розв’язків та структура загального розв’язку.

Тема 1.6. Система n лінійних рівнянь з n невідомими

1.  Метод оберненої матриці розв'язування системи рівнянь.

2.  Правило Крамера розв'язування системи рівнянь.

3.  Умови сумісності та несумісності, визначеності і невизначеності системи рівнянь у термінах визначників.

4.  Умова існування ненульового розв’язку однорідної системи рівнянь.

Література:

[1], т. І, с. 99-117.

[2], с. 129-152.

[3], с. 31-64.

Задачі, рекомендовані до розв’язання:

[1], т. І, с. 106, № 1-2, с. 117, № 1-8.

[2], с. 198, № 1-3, 10-31.

[3], с. 79, № 1.85-1.86.

Питання для самоконтролю

1)  Що називається рішенням системи лінійних рівнянь? Які системи називаються сумісними, а які – несумісними?

2)  Напишіть формули Крамера. У якому випадку вони застосовні?

3)  За якої умови система лінійних рівнянь має єдине рішення?

4)  Що можна сказати про систему лінійних рівнянь, якщо її головний визначник рівний нулю?

5)  З яких елементарних кроків складається процедура перетворення системи рівнянь методом Гауса?

6)  Чому в результаті перетворення системи рівнянь методом Гауса виходить система рівнянь, еквівалентна початковій системі?

7)  Як в результаті перетворення системи рівнянь методом Гауса визначити, чи сумісна початкова система лінійних рівнянь?

8)  Як, користуючись методом Гауса, визначити, чи має початкова система рівнянь єдине рішення?

9)  Поняття системи m рівнянь з n невідомими та запис її у матричній формі.

10)  Ранг матриці та його зв’язок з лінійною незалежністю рядків (стовпців) матриці.

11)  Елементарні перетворення матриці та обчислення за їх допомогою рангу матриці.