Первичная обработка статистических данных. Практическое пособие, страница 9

Заметим, что из равенства нулю вероятности конкретного значения х не следует невозможность принятия случайной величины Х этого значения. Так как непрерывная случайная величина имеет бесконечное множество значений, то каждое из них реализуется крайне редко.

Поэтому для непрерывных величин определяется вероятность попадания значений в бесконечно малый интервал ∆х. Эта вероятность вычисляется по формуле:

P(х  ≤  Х < х + ∆х) = F_x(x + ∆x) – F_x(x).

Долю вероятности, соответствующую единице длины интервала ∆х, показывает соотношение:

.

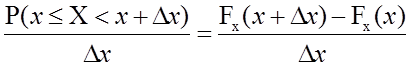Очевидно, что предел этого соотношения при ∆х→0 является производной функции распределения:

.

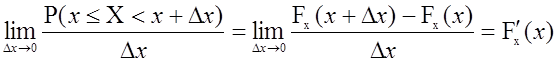Определение 1.11 Плотностью распределения вероятностей  р_х(х)  непрерывной случайной величины Х называется первая производная (если она существует) ее функции распределения:

р_х(х) = F΄_х(х).

Плотность распределения вероятностей р_х(х) сокращенно называют плотностью вероятности случайной величины Х. Иногда вместо термина «плотность вероятности» используется эквивалентный термин «дифференциальная функция распределения». Случайная величина имеет функцию плотности вероятности только тогда, когда ее функция распределенияF_х(х) непрерывна и дифференцируема всюду, за исключением отдельных точек на конечном промежутке. Функция плотности вероятности р_х(х) дает возможность судить о характере распределения непрерывной случайной величины в малых окрестностях точек числовой оси.

Из предшествующих рассуждений следует, что плотность вероятности р_х(х) пропорциональна вероятности того, что случайная величина примет значение, находящееся на бесконечно малом расстоянии  ∆х→0  от точки  х.  Отсюда также вытекает следующее приближенное равенство:

Р(х ≤  Х < х + ∆х)  ≈  р_х(х ) ∆х.

Произведение р_х(х)∆х  называют элементом вероятности, оно равно площади прямоугольника с основанием ∆х и высотой  р_х(х). Значит, вероятность попадания значений случайной величины Х в полузамкнутый интервал  [х; х + ∆х)  приближенно равна площади прямоугольника с основанием  ∆х  и высотой, равной  р_х(х ).

Рассмотрим геометрическую интерпретацию данного утверждения.

∆х

рх(х )

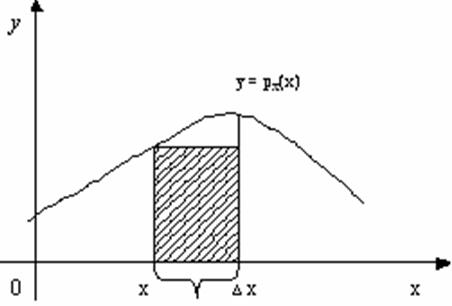
Рисунок 1.3 – Вероятность попадания значений случайной

величины Х в интервал [х; х + ∆х)

Площадь заштрихованного прямоугольника приближенно равна вероятности того, что случайная величина Х примет значение, принадлежащее интервалу  [х; х + ∆х).

Рассмотрим основные свойства плотности вероятности.

1.  Плотность вероятности  р_x(х)  всегда неотрицательна:

р_х(х) ≥  0.

2.  Вероятность того, что непрерывная случайная величина Х примет значения из интервала [х₁; х₂) вычисляется по формуле:

.

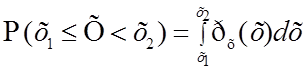3. Для плотности вероятности всегда справедливо равенство:

.

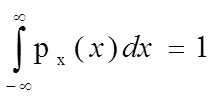4. Функция распределения F_х(х) и плотность вероятности р_x(х) непрерывной случайной величины Х связаны формулой: 

.

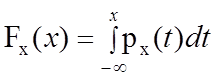Рассмотрим геометрическую интерпретацию основных свойств плотности вероятности.

y = px(x)

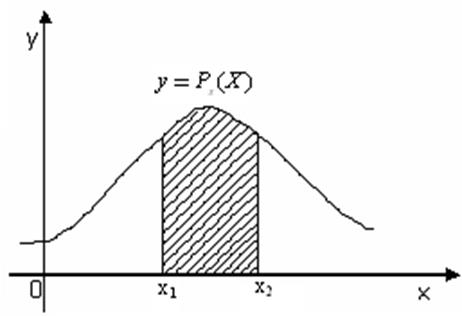
Рисунок 1.4 – Вероятность попадания значений случайной           величины Х в интервал [х₁; х₂)

Данный рисунок показывает, что в соответствии со вторым свойством площадь заштрихованной криволинейной трапеции, заключенной между кривой плотности вероятности  y = p_x(x)  и осью О_х,  равна вероятности неравенства   P(х₁ ≤  Х  < х₂).

у = px(x)

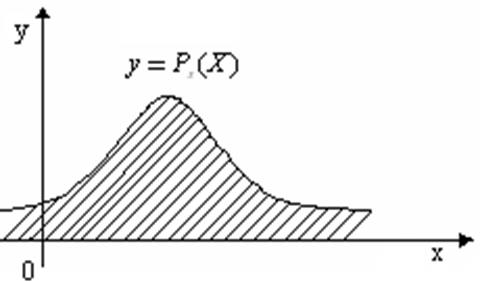
Рисунок 1.5 – Полная площадь

под кривой плотности вероятности

Так как по третьему свойству плотности

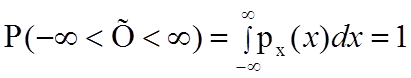, то площадь заштрихованной фигуры, ограниченной графиком плотности вероятности  y = р_х(х)  и осью  О_х , всегда равна 1, что показывает рисунок 1.5.

Так как функция распределения F_х(х) равна вероятности того, что случайная величина Х примет значения, меньшие числа х, то по свойству 4 имеем:

.

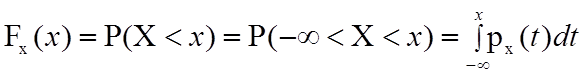Следовательно, геометрически функция распределения F_х(х)  равна площади заштрихованной фигуры на рисунке 1.6, расположенной левее точки  х, ограниченной графиком плотности вероятности  y = р_х(х)  и осью  О_х.