Первичная обработка статистических данных. Практическое пособие, страница 18

Алгоритм вычисления моды статистического ряда

Условие: длина каждого интервала статистического ряда одинакова.

1.  Определяется модальный интервал статистического ряда.

Будем считать, что именно i-й интервал  имеет наибольшую частоту, то есть является модальным. Вместе с ним также рассматриваются предыдущий ()-й интервал  и последующий -й  интервал  . 

2. Для каждого из этих интервалов находятся соответствующие частоты:

.

3.  Значение моды вычисляется по формуле:

.

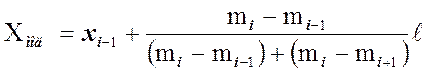Подчеркнем, что  – это нижняя граница модального интервала,  – частота предшествующего ему интервала,  – частота последующего интервала,  – длина каждого интервала.

Пример 2.2 Найдем моду статистического ряда по данным примера 1.7  о возрасте пациентов клиники.

Таблица 2.2 – Данные исследования возраста пациентов           поликлиники

Очевидно, что наибольшую частоту имеет пятый интервал [50; 60), для которого . Частота предыдущего интервала , частота последующего интервала  , длина каждого интервала   = 10. Тогда мода вычисляется по формуле:

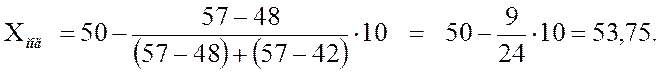
Учитывая, что выборочные данные характеризуют возраст пациентов в годах, округляем найденное значение:

.

Таким образом, чаще других обращаются в поликлинику пациенты в возрасте от 50 до 60 лет, причем в этой группе наиболее проблемный возраст составляет 53,75 года.

■

Мода – одна из немногих характеристик, которая используется при анализе не только количественных, но и качественных данных.

Пример 2.3 Рассмотрим данные анкетирования 40 посетителей автосалона о предпочитаемом ими цвете автомобиля:

Таблица 2.3 – Результаты анкетирования о любимом цвете            автомобиля

В этой выборке модой является белый цвет, имеющий наиболь- шую частоту.

■

Понятие моды используется главным образом в прикладных исследованиях тогда, когда возникает необходимость выявления в выборке большого объема наиболее преобладающих вариант. Такие ситуации часто встречаются при изучении потребительского спроса, качественного состава продукции массового производства, результатов опроса населения и в других случаях. Но так как мода не всегда существует, то в аналитической статистике это понятие используется крайне редко.

Результаты многочисленных исследований показывают, что значительная часть выборочных данных имеет тенденцию собираться вокруг некоторого центра. Это свойство обобщается введением следующего понятия медианы.

Определение 2.2Пусть все выборочные данные x₁, x₂, …, x_n расположены в порядке возрастания с сохранением повторяющихся значений. Если n– нечетное число, то медианой этой выборки называется число X, равное выборочному           значению 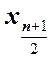 ,  стоящему на 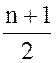-м  месте. Если n– четное число, то медиана Х  равна полусумме выборочных значении  и 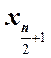, стоящих соответственно на  -м   и 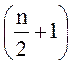 -м  местах:

Х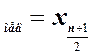 при нечётном n;   X =  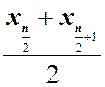  при чётном  n.

Другими словами, если объем выборки является нечетным числом, то медиана Х равна единственному выборочному значению, расположенному в самой середине упорядоченной выборки. Если же объем выборки является четным числом, то посередине выборки находятся два соседних значения. В этом случае медиана равна сумме этих значений, деленной на 2.

Пример 2.4 Ниже приводятся две выборки данных о количестве новых слов, выученных каждым из девяти учеников одной группы и каждым из десяти учеников другой группы в течение одного урока английского языка.

I группа: 1,   3,   3,   4,   4,   5,   6,   7,   8.

II группа: 1,   2,   2,   3,   3,   5,   5,   6,   6,   7.

Обе выборки записаны в порядке возрастания их значений. Объем первой выборки n = 9 является нечетным числом, поэтому посередине находится одно пятое значение , которое и         является медианой этой выборки: