Первичная обработка статистических данных. Практическое пособие, страница 31

Найдем третий квартиль . Так как 75 > 50, то берем значение . Для    найдено два целых числа    и  . На 10-м и 11-м местах от конца выборки стоят  соответствующие значения  и . Вычислим их полусумму 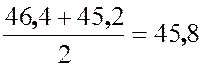. Полученное число и является 75-м процентилем. Следовательно,  .

Теперь вычислим 37-ой процентиль. Найдем 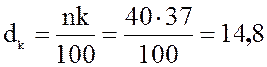 . Округлим до следующего целого: . На 15-м месте от начала выборки находится значение 22,5, которое и является 37-м процентилем: .

Квартили , ,  делят выборку на четыре равные части:

■

Сгруппированные по интервалам наблюдения скрывают конкретные выборочные значения, поэтому точные значения процентилей и квартилей не определяются. По статистическому ряду можно найти только их приближенные оценки. Метод нахождения оценок процентилей объясняет следующий конкретный пример.

Пример 2.32   Рассмотрим сведения о сроках эксплуатации        50 легковых автомобилей, зарегистрированных страховой фирмой.

Таблица 2.22  –Данные о сроках эксплуатации автомобилей

В третьей строке даны процентные количества выборочных значений в каждом интервале.

Простроим гистограмму данного статистического ряда.

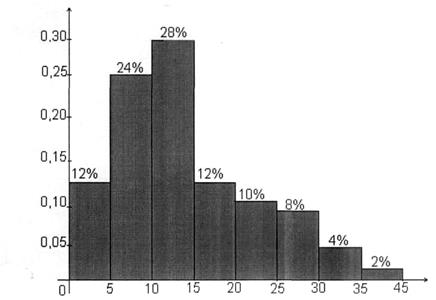
Рисунок 2.3  – Гистограмма данных о сроках эксплуатации

автомобилей

Будем считать, что внутри каждого интервала выборочные значения распределены одинаково равномерно. Это значит, что всем элементам интервала соответствуют отрезки одинаковой длины. Например, первый интервал содержит 12 % выборочных значений, тогда одному проценту соответствует отрезок длиной  ,  где          – длина интервала.

Чтобы найти k-ый процентиль статистического ряда, необходимо, прежде всего, выяснить, в каком интервале он находится. Допустим, мы хотим найти 70-й процентиль  . Последовательно складываем проценты  1-го,  2-го, … интервалов до тех пор, пока не получим максимальную сумму, не превосходящую числа 70:

12 %  + 24 %  + 28 %  = 64 %.

Следовательно, 70-й процентиль попадает в следующий четвертый интервал (15–20]. Чтобы получить 70 %  надо к 64 %  прибавить 6 %  значений из четвертого интервала. В четвертом интервале содержится 12 %  значений, длина его равна 5, поэтому каждому проценту соответствует  длина  , но тогда 6 %  значений         лежит на отрезке, длина которого равна 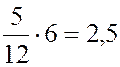 . Прибавляем  к нижней границе интервала это значение 15 + 2,5 = 17,5. Полученное число и является 70-м процентилем: . Это означает, что все выборочные значения из первого, второго и третьего интервалов и не более 6 %  значений из четвертого интервала являются меньшими числа  .

■

В том случае, когда выборка не сгруппирована и упорядочена по возрастанию от меньшего к большему, каждому значению выборки соответствует  определенный процентный ранг. Рассмотрим это понятие на конкретном примере.

Пример 2.33   Найдем процентный ранг каждого элемента    следующей выборки, характеризующей количественный состав  10 семей:

1,  2,  2,  3,  3,  3,  3,  4,  4,  5.

Рассмотрим значение, равное 2. В выборке только одно значение меньше 2-х, что составляет 10 %  всей выборки. После значения 2 следующим выборочным значением является 3. В выборке есть три значения, которые меньше 3-х, что составляет 30 %  всей выборки. Складываем 10 %  + 30 %  и делим на 2, полученное число 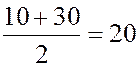  и будет процентным рангом выборочного значения 2, обозначаемого символом  .