Первичная обработка статистических данных. Практическое пособие, страница 24

Степень различия между отдельными значениями генеральной совокупности или между выборочными значениями называется изменчивостью, или вариацией. Аналогичный смысл вкладывается в такие понятия, как рассеяние и разброс.

Рассмотрим три основных характеристики степени изменчивости статистических данных.

Самым простым показателем изменчивости является вариационный размах.

Определение 2.9 Вариационным размахом выборки  x₁, x₂, …, x_n называется число R, равное разности между наибольшим и наименьшим значениями данной выборки:

Вариационный размах может называться одним словом – размах.

Пример 2.19 Рассмотрим метеорологические данные о дневной температуре воздуха за одну неделю наблюдений:

Размах этой выборки легко находится:

.

■

Фактически, размах дает максимальную величину отклонения между выборочными значениями.

Определение 2.10 Диапазоном наблюдений выборки  x₁, x₂, …, x_n называется отрезок , заключенный между              минимальным выборочным значением  и максимальным  .

Диапазон наблюдений содержит все выборочные значения. Например, отрезок    является диапазоном наблюдений для выборки температуры воздуха за неделю наблюдений.

Заметим, что размах равен длине диапазона наблюдений.

Так как размах находится лишь по двум экстремальным выборочным значениям, то он не дает информации об изменчивости остальных наблюдений. Размах, в основном, используется для выборок небольшого объема, он дает слишком поверхностное представление об изменчивости исследуемого явления.

В отличие от размаха следующая числовая характеристика является показателем изменчивости внутри диапазона наблюдений. Рассмотрим отклонения всех выборочных значений   от среднего  этой выборки:

,       ,     … , .

Некоторые из этих отклонений являются положительными числами, а другие отрицательными, при этом сумма всех отклонений равна  0  для любой выборки. Заметим, что модуль отклонения           =  равен расстоянию между выборочным значением  и средним . Тогда сумма модулей отклонений учитывает все случайные выборочные значения и является положительным числом. Чем теснее выборочные значения группируются вокруг среднего, тем меньше эта сумма, и, наоборот, при широком разбросе выборочных значений сумма модулей отклонений увеличивается. Среднее значение суммы модулей отклонений характеризует усредненное расстояние выборочных значений от центра.

Определение 2.11  Средним абсолютным отклонением выборки  x₁,  x₂,  …,  x_n   со средним    называется число  ,  которое вычисляется по формуле:

.

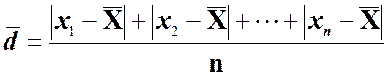В сокращенном виде данное выражение записывается так:

.

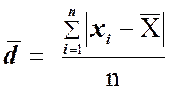Среднее абсолютное отклонение, которое называется также средним линейным отклонением, является простой и полезной характеристикой степени рассеяния выборочных данных. К сожалению, из-за определенных неудобств при работе с модулями              величин это понятие не используется в теоретической статистике.

Пример 2.20 Рассмотрим выборочные данные о годовой стоимости обучения в восьми вузах города:

900, 1200, 1500, 1700, 1800  2100, 2400,  2800.

Найдем среднее абсолютное отклонение этой выборки. Прежде всего, вычислим среднее:

.

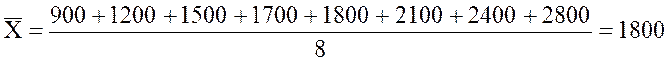Определим отклонения всех выборочных значений:

Для проверки правильности расчетов можно использовать равенство:

Теперь вычислим:

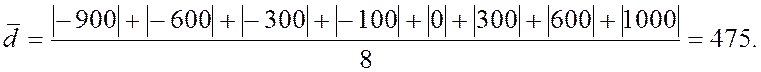
Итак, среднее абсолютное отклонение стоимости обучения в данных вузах равно 475. Заметим, что реальные отклонения могут быть меньше или больше среднего отклонения.

■

Основными характеристиками степени рассеяния выборочных данных являются дисперсия и стандартное отклонения.

Определение 2.12  Дисперсией выборки x₁, x₂, …, x_n  называется число  ,  которое вычисляется по формуле:

   

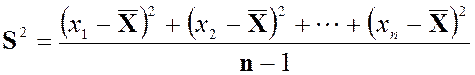
при малом объеме выборки  (n ≤ 30)  и

 

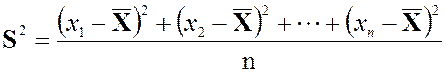
при большом объеме выборки  (n > 30).

Сокращенно формулы записываются в таком виде:

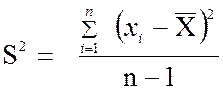   или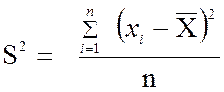 

Выборочная дисперсия при малых значениях объема n ≤ 30 и при больших значениях n > 30 вычисляется по разным формулам. Замена делителя  n  на  n – 1 для выборок малых объемов устраняет систематическую ошибку, или «смещение» относительно дисперсии всей генеральной совокупности. Исключение систематической ошибки – это одно из необходимых условий получения правильной оценки любой числовой характеристики генеральной совокупности.