Первичная обработка статистических данных. Практическое пособие, страница 14

В теории вероятностей рассматриваются и изучаются вероятностные законы распределения случайных величин. Как правило, любое вероятностное распределение случайной величины задается в аналитическом виде каким-либо математическим выражением.  В математической статистике рассматриваются статистические распределения. Ранее мы говорили о близости понятия статистического ряда с понятием статистического распределения выборки. На практике часто возникает задача нахождения аналитического выражения, которое, хотя бы приближенно, представляло бы неизвестную теоретическую функцию распределения исследуемой случайной величины. В математической статистике рассматривается аналог этой функции.

Определение 1.19 Если x₁, x₂, …x_n– выборка значений случайной величины Х, то эмпирической функцией распределения называется функция действительного аргумента  xÎ (- ∞; ∞), обозначаемая через , равная относительной частоте            выборочных значений, меньших числа  x .

Таким образом,

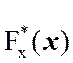 = , где   n  – это объем выборки значений случайной величины Х, а           n_x – это количество   выборочных значений, удовлетворяющих    неравенству  Х < x,   xÎ (- ∞; ∞).

Так как относительная частота значений случайной величины  Х, удовлетворяющих неравенству  Х < x,  в выборке объема n  стремится к вероятности выполнения этого  неравенства, то при         n →  ∞  имеем, что

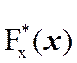=   →  P(X < x) = F_х(x).

Таким образом эмпирическая функция распределения стремится к теоретической функции распределения. Чем больше объём выборки, тем точнее оценивается теоретическое распределение выборочными данными. Данный вывод обосновывается следующей теоремой В. И. Гливенко, которая считается фундаментальной теоремой математической статистики.

Теорема 1.1 Если   и   – теоретическая и эмпирическая функции распределения для выборки объема  n,  то для любого  ε > 0 

P( | F_х(x) –  | < ε) = 1.

Аналитическое выражение эмпирической функции распределения хорошо находится по данным вариационного ряда. Для этого определяются значения функции для всех вариант выборки.

Пример 1.14 Найдем эмпирическую функцию распределения по данным вариационного ряда из примера 1.6 о посещаемости университетской библиотеки.

Таблица 1.8 – Вариационный ряд данных посещаемости библиотеки

Объём данной выборки  n= 25. По определению 1.19 находим значения эмпирической функции распределения для всех вариант

;

;

;

;

;

;

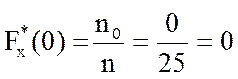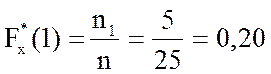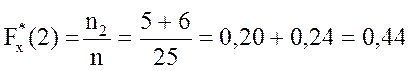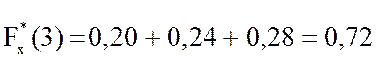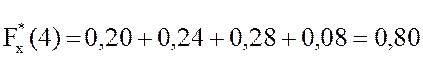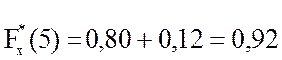для  x> 5   .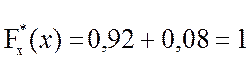

Объединим полученные результаты и найдем выражение               для  .

   

y

Построим графическое изображение данной функции.

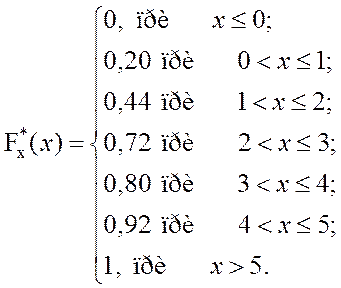
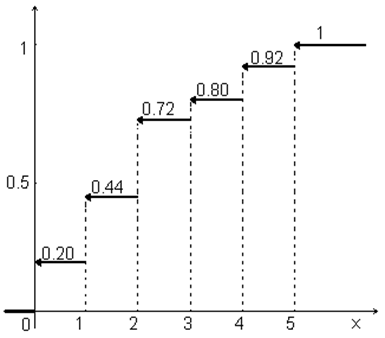
Рисунок 1.13 – График эмпирической функции распределения

посещаемости библиотеки студентами

■

Интервальный статистический ряд скрывает конкретные выборочные значения случайной величины. Поэтому точные значения эмпирической функции распределения  можно определить только на границах интервалов, внутри интервалов при отсутствии полной информации о выборочных данных значения эмпирической функции распределения можно определить только приближенно. В том случае, когда исследуется непрерывная случайная величина, то в системе координат отмечаются найденные значения эмпирической функции распределения на границах интервалов и полученные точки последовательно соединяются плавной линией. В результате получается  приближенный график эмпирической функции распределения.

Пример 1.15 Построим эмпирическую функцию распределения  по данным статистического ряда из примера 1.8 обследования высот городских зданий.

Ранее мы получили следующий статистический ряд: