Первичная обработка статистических данных. Практическое пособие, страница 11

а = <  <  < … <  = b.

Для каждого i-го интервала  [; ),  = 1,2,…, k,  найдём частоту  ,  равную числу выборочных значений, принадлежащих этому интервалу. Частное    является относительной частотой выборочных значений, принадлежащих i-му интервалу. Используем стандартное обозначение:  =.

Очевидно, что сумма частот всех интервалов равна объему выборки:

, а сумма всех относительных частот равна 1:

.

Определение 1.16 Таблица интервалов, содержащая данную выборку значений случайной величины Х и соответствующие частоты или относительные частоты, называется статистическим рядом.

В общем случае статистический ряд представляется следующим образом.

Таблица 1.5 – Интервальный статистический ряд

Интервалы значений Х	[x0; x1)	[x1; x2)	…	[]
			…
			…

Заметим, что вариационный ряд является частным случаем    статистического ряда.

Пример 1.7  Администрацией поликлиники  были собраны данные о возрасте 250 наиболее нуждающихся в лечении пациентов. Результаты этого исследования представлены следующим статистическим рядом.

Таблица 1.6 – Данные исследования возраста пациентов поликлиники

Следующие суммы находятся для проверки вычислений:

■

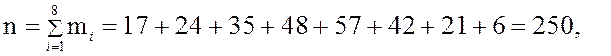
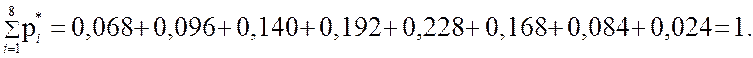
Рассмотрим общую последовательность действий при построении статистического ряда.

Алгоритм построения статистического ряда

случайной выборки

1.  Заранее определяется число интервалов  k.

Число интервалов можно выбирать произвольно, оно не должно быть слишком большим и слишком малым. Можно воспользоваться известной оценочной формулой:

k  ≈ 1 + 3,2 lgn, где правая часть равенства округляется до ближайшего целого.

2.  Определяется длина интервала.

Для этого вычисляется число

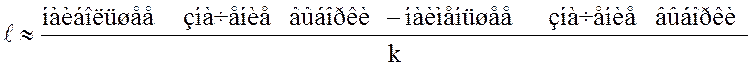
при этом значение  округляется так, чтобы получилось простое и удобное число.

3.  Определяется начало и конец всего интервала наблюдений, содержащего всю данную выборку.

Число а, обозначающее нижнюю границу, должно быть чуть меньше, чем наименьшее выборочное значение. Число b, обозначающее верхнюю границу, находится по формуле:

b =  ∙ k , где  – длина интервала, k – число всех интервалов.

4. Находится частота каждого интервала, равная числу        выборочных значений, принадлежащих этому интервалу.

При этом пограничные значения приписываются только одному интервалу. В результате получится k значений:

,,…,,  причем  .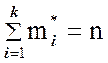

5.  Вычисляются соответствующие  относительные частоты:

,  , … , .

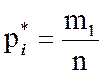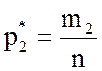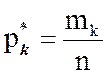Для проверки находится их сумма: .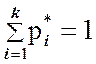

6. Полученные результаты заносятся в таблицу представляющую статистический ряд.

Пример 1.8  Составим статистический ряд по данным измерений высот 40 зданий города.

7,2	15,2	20,8	24,6	27,5	30,6	34,7	38,5
9,6	16,3	22,4	25,1	28,3	31,8	35,6	42,3
10,5	17,2	23,5	25,7	28,8	32,3	35,8	43,4
12,8	18,4	23,7	26,4	29,4	33,2	36,2	44,5
14,2	18,8	24,5	27,2	30,4	34,5	37,4	48,5

Будем строить статистический ряд для девяти интервалов:             k = 9, n = 40.

Наименьшее выборочное значение равно 7,2 , наибольшее – 48,5. Определим длину каждого интервала. Найдем 

 =.

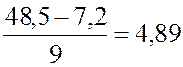Округлив полученное число до ближайшего целого, будем считать, что длина интервала  = 5.

В качестве нижней границы всех наблюдаемых значений выберем число 5. Тогда имеем следующие интервалы: