Первичная обработка статистических данных. Практическое пособие, страница 27

Таким образом, не менее 75 % значений случайной величины имеют отклонение от среднего μ, не превышающее двух стандартных отклонений  2s, и не менее 89 % значений отличаются от среднего не более чем на три стандартных отклонения 3s.

Конкретные значения случайных величин с нормальным распределением имеют еще более выраженную центральную тенденцию. Многочисленные статистические исследования стали основанием для следующего утверждения, подходящего для многих реальных выборок.

Если  – среднее, а S – стандартное отклонение выборки , то в интервале  содержится около 68 % выборочных значений, в интервале  содержится около 95 % выборочных значений, в интервале   содержится около 99,7 % выборочных значений.

Другими словами, около 68 % выборочных значений имеют          отклонение от среднего, не превышающее одного стандартного отклонения S, около 95 % выборочных значений имеют отклонения не более 2S, а между значениями  находится около 99,7 % выборки.

Пример 2.26 В примере 2.24 мы нашли   метров и    метров для высоты 40 зданий.

Рассмотрим интервал . Вернемся к первоначальным не сгруппированным данным примера 1.4 и подсчитаем, сколько выборочных значений содержится в этом интервале. Их оказалось 27, что составляет 67,5 % от объема всей выборки.

Рассмотрим интервал , он содержит 39 выборочных значений, что составляет 97,5 % от всей выборки. И только одно значение не попало в этот интервал.           В интервал  попадает вся выборка.      

     ■

В любом случае полученные по конкретным выборкам значения среднего  и стандартного отклонения S не совпадают с соответствующими  значениями среднего μ и стандартного отклонения  всей генеральной совокупности. С одной стороны возникает вопрос о степени согласованности между выборочными и теоретическими характеристиками исследуемой случайной величины, с другой – об оценке достоверности характеристик, найденных по конкретной единичной случайной выборке. Для каждого параметра распределения существуют так называемые стандартные ошибки, которые дают возможность по результатам одной выборки оценивать параметры других выборок исследуемой совокупности. Так, например, стандартной ошибкой среднего  называется  отношение стандартного отклонения  S  к  , где  n – объем выборки, то есть величину ,  равную

.

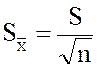Очевидно, что значение стандартной ошибки существенно зависит от объема выборки  n. Величина стандартной ошибки приблизительно показывает, насколько среднее    одной выборки отличается от средних других выборок объема   n  из исследуемой генеральной совокупности.

Стандартная ошибка  всегда меньше стандартного отклонения S, которое характеризует изменчивость отдельных значений относительно среднего    внутри одной выборки.

Степень рассеяния выборочных значений случайной величины также показывает следующая относительная характеристики.

Определение 2.16Коэффициентом вариации выборки         x₁,  x₂, …, x_n называется отношение её стандартного отклонения   S   к среднему  :

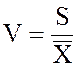,    где.

Определение 2.17 Коэффициентом вариации случайной          величины  X  называется отношение её стандартного отклонения  к математическому ожиданию μ:

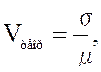    где   .

Заметим, что при   = 1   и   μ = 1  получаем, соответственно, что  V = S  и V_теор = . Часто выборочный и теоретический коэффициенты вариации задаются в процентах:

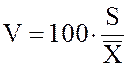 %   и   .

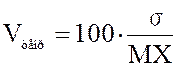Во всех случаях коэффициент вариации является безразмерной относительной характеристикой рассеяния значений случайной величины, которая используется для сравнения нескольких выборок из генеральной совокупности одного типа.

Пример 2.27  Найдем коэффициент вариации высот городских зданий по данным примера 2.24.

Ранее мы нашли, что    = 27,125  и  S = 9,961. Тогда выборочный коэффициент вариации 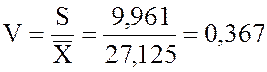 ,  что составляет около 37 %.                                                                       

■

2.5  Выборочные и теоретические моменты

распределения

Рассмотрим важные выборочные числовые характеристики распределений, обобщающие понятия среднего и дисперсии. Пусть  k – целое неотрицательное число.

Определение 2.18  Начальным моментом  k-го  порядка        выборки   x₁,  x₂, …,  x_n   называется среднее  k-тых степеней данных выборочных значений, то есть