Первичная обработка статистических данных. Практическое пособие, страница 19

X_мед(I) = 4.

Посередине второй выборки находятся два значения 3 и 5,          поэтому

Х.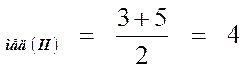

Значит, эти выборки имеют равные медианы  X_мед = 4.

■

Медиана делит выборку на две части, каждая из которых содержит одинаковое количество элементов. Первая часть состоит из выборочных значений, расположенных до медианы. Их величина не может быть больше величины медианы. Вторую часть составляют выборочные значения, расположенные после медианы. Их величина не может быть меньше величины медианы. Например, медиана  Х  из предыдущего примера показывает, что половина учеников каждой группы за урок выучила не более 4-х новых английских слов, а вторая половина запомнила не менее 4-х слов. Таким образом, медиана является определенным граничным значением исследуемой случайной величины, показывающим, что в половине всех испытаний получаются выборочные значения, не превосходящие медиану, а в половине испытаний получаются значения, практически  превосходящие медиану по величине. Фактически медиана выборки характеризует структуру и конфигурацию составляющих элементов исследуемой совокупности.

Теперь рассмотрим способ нахождения медианы по сгруппированным данным.

Таблица 2.4  – Произвольный статистический ряд

Алгоритм вычисления медианы статистического ряда

Условие: длина каждого интервала статистического ряда равна .

1. Прежде всего, определяется так называемый медианный интервал. Для этого вычисляется число , равное половине всего количества выборочных значений. Затем последовательно складываются частоты первого, второго и так далее интервалов до тех пор, пока не получится сумма, которая либо равна  ,  либо чуть больше  .  Интервал, соответствующий последней прибавленной частоте, и будет являться медианным. Допустим, что сумма частот первых  s  интервалов не меньше числа  ,  то есть

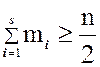, но сумма частот нижних  s – 1 интервалов меньше  ,  то есть

.

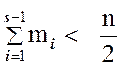Тогда именно s-й интервал    является медианным.

2. Далее медиана статистического ряда вычисляется по формуле:

Х.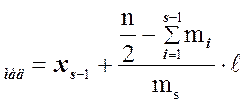

Подчеркнем, что  – это нижняя граница медианного интервала, n – объем всей выборки, 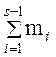– сумма частот всех интервалов, расположенных ниже медианного,   – частота медианного интервала,   – длина каждого интервала.

Пример 2.5  Найдем медиану статистического ряда по данным о возрасте пациентов поликлиники.

Таблица 2.5 – Данные исследования о возрасте пациентов             поликлиники

Объем всей выборки n = 250, поэтому  = 125. Последовательно складываем частоты пока не получим сумму, равную или большую 125:

17 + 24 + 35 + 48 = 124,   но

17 + 24 + 35 + 48 + 57 = 181.

Сумма частот первых четырех интервалов меньше 125, а сумма частот пяти интервалов больше 125, поэтому именно пятый интервал  [50; 60)  является медианным. Вычислим медиану по данной формуле:

Х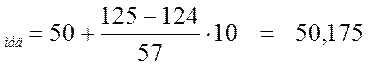

или

Х.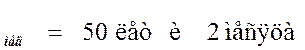

Это значение медианы показывает, что возраст половины пациентов в данной  выборке не больше 50 лет и 2 месяцев.

■

Пример 2.6  Найдем медиану статистического ряда из примера  1.8, представляющего данные о высоте зданий.

Таблица 2.6  – Статистический ряд измерений высоты зданий

Объем всей выборки , поэтому  = 20. Находим последовательно суммы частот:

          2 + 3 + 5 + 6 = 16 < 20,

но    2 + 3 + 5 + 6 + 8 = 24 > 20.

Поэтому пятый интервал   [25; 30)  является медианным.

Вычислим медиану по указанной выше формуле:

Х.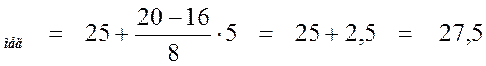

Следовательно, X_мед = 27,5. Это значение показывает, что в            исследуемой выборке половина зданий имеет высоту не более 27,5 метров.