Первичная обработка статистических данных. Практическое пособие, страница 32

Рассмотрим значение 3. В выборке имеется три значения меньших 3-х, что составляет 30 %  выборки, и семь значений меньших 4-х, что составляет 70 %. Получаем процентный ранг

.

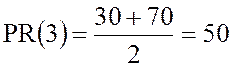Рассмотрим значение 4. В выборке 7 значений меньших 4-х (70 %) и 9 значений меньших 5-ти (90 %), поэтому  .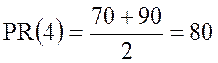

Рассмотрим значение 1. В выборке нет значений меньших 1 (0 %) и одно значение меньше 2-х (10%), поэтому  .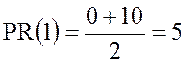

Наконец возьмем значение 5. В выборке 90 %  значений меньших 5 и 100 %  значений меньших следующего  условного значения, поэтому  .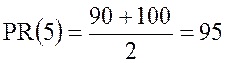

Таким образом, мы нашли процентные ранги всех выборочных значений:

,   ,   ,   ,   .

Простые вычисления дают следующие значения соответствующих процентилей:

■

Рассмотрим понятие процентного ранга в общем виде.

Определение 2.27 Пусть x– произвольное значение, имеющее частоту m  в упорядоченной выборке объёма n. Процентным рангом значения  x называется число  , равное

,

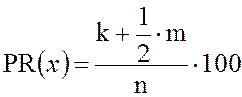где  k– число выборочных значений, меньших x.

Например, для предыдущей выборки найдем процентный ранг значения 4:

.

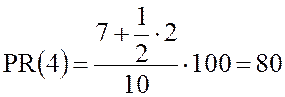Заметим, что понятие процентиля (персентиля) совпадает с понятием процентной точки. Процентили, или процентные точки используются для обозначения границ изменчивости исследуемой случайной величины. Несколько значений процентилей могут довольно хорошо показать основные черты распределения. Наиболее часто используются пять основных процентелей:

1. Наименьшее выборочное значение, или нулевой процентиль: .

2. Первый нижний квартиль , совпадает с 25-м процентилем: .

3. Медиана, совпадающая со вторым квартилем и с 50-м процентилем: .

4. Третий верхний квартиль, или 75-й процентиль: .

5. Наибольшее выборочное значение, или 100-й процентиль .

Пример 2.34 Рассмотрим данные измерений частоты пульса             у двенадцати пациентов поликлиники:

58,  62,  64,  65,  72,  74,  78,  80,  82,  84,  88,  93.

Наименьшим значением является 58, а наибольшим – 93.

Найдем медиану. Так как   – четное число, то берем два значения  = 6  и 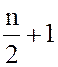  = 7. На 6-м и 7-м местах находятся значения  и  . Медиана  .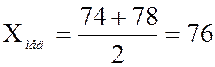

Найдем первый квартиль . Итак,  и 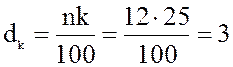  является целым числом, поэтому берем два числа    и  . На 3-м  и 4-м местах от начала выборки находятся    и   . Тогда  .

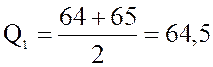Для определения верхнего квартиля    берем значения 84 и 82, стоящие на 3-м  и  4-м местах от конца выборки. Тогда  .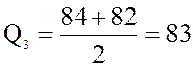

Следовательно, мы получили пять основных показателей локализации выборочных значений:

   ;       и 

■

Подчеркнем, что пять основных процентилей делят выборку на четыре части, содержащих по 25 % выборочных значений. Квартили   и   выделяют центральную часть выборки, которая, как считается, дает более устойчивые оценки исследуемого распределения.

Статистическое понятие процентиля тесно связано со следующим теоретическим аналогом.

Определение 2.28  Квантилью порядка p, или p-квантилью, , случайной величины X с функцией распределения  называется число  x_p,  для которого

.

Это значит, что p-квантиль  является корнем данного уравнения. Из определения функции распределения следует, что значение pявляется вероятностью события  . Отметим, что             0,5-квантиль совпадает с медианой . Если функция распределения  строго монотонна, то уравнение имеет только одно решение, причем большим значениям вероятностей pсоответствуют большие значения квантилей. Если случайная величина Х является дискретной, то ее функция распределения изменяется скачками, поэтому для некоторых значений  p  решения указанного уравнения образуют целый отрезок между двумя соседними  и , такими, что , но . При этом любая точка отрезка    является p-квантилью.

Подчеркнем, что квантиль порядка pсовпадает с k -ым процентилем при k = 100 p. Квантили и процентили связаны следующим соотношением:

.

Таким образом, 0,95-квантиль является 95-ым процентилем; соответственно, квантили

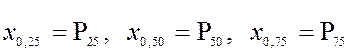
также называются квартилями. Квантили  и соответствующие процентили называются децилями. Для ряда наиболее известных законов распределений составлены специальные таблицы, по которым находятся значения квантилей и, соответственно, процентилей.